在平均数的计算公式中,每个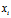 都有相同的重要性或权重。但有时候,计算平均数时会对每个观测值赋予显示其重要性的权重。以这种方式计算的平均数称做加权平均数。
都有相同的重要性或权重。但有时候,计算平均数时会对每个观测值赋予显示其重要性的权重。以这种方式计算的平均数称做加权平均数。
加权平均数:

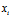 ——第
——第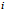 个观测值的数值;
个观测值的数值;
 ——第
——第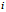 个观测值的权重;
个观测值的权重;
举个例子来说明什么时候需要使用加权平均数。下面是一个公司在过去3个月5次购买原材料的样本。
购买批次 | 价格(美元/磅) | 数量(磅) |
1 | 3.00 | 1200 |
2 | 3.40 | 500 |
3 | 2.80 | 2750 |
4 | 2.90 | 1000 |
5 | 3.25 | 800 |
我们注意到,每磅价格在2.80~3.40美元之间变化,而且采购数量也在500~2750磅之间变化。假设我们想知道原材料每磅平均价格的有关信息,因为订购的数量各不相同(可能存在量大从优的情况),我们必须要使用加权平均数。计算每磅价格的平均数时,要根据每个价格对应的数量来加权。在本例中,五个权重分别是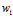 =1200、
=1200、 =500、
=500、 =2750、
=2750、 =1000、
=1000、  =800。计算加权平均数如下:
=800。计算加权平均数如下:

于是,使用加权平均数计算原材料每磅的平均价格是2.96美元。如果不是使用加权平均数公式而是使用平均数公式计算,结果为 美元,得到带有误导性的结果,夸大了每磅实际的平均价格。
美元,得到带有误导性的结果,夸大了每磅实际的平均价格。
在某个特定的加权平均数计算中,对权重的选择依赖于具体的应用。在任何情况下,当观测值的重要性变化时,分析人员必须选择能够最好反映每个观测值重要性的权重,来计算加权平均数。