从一道简单的几何题说起

简单题

今天在《单墫初中数学指津——平面几何的知识与问题》上看到一道简单的几何题：

若( riangle ABCsim riangle ADE), 则 ( riangle ABD sim riangle ACE).

做完这个题目我都没看第二眼，它实在太平凡了。直到看到下面定理的解答时，我才注意到这个题目居然在其中出现了。

托勒密定理

(托勒密(Ptolemy))对四边形 (ABCD), 必有 (ABcdot CD+ADcdot BCgeq ACcdot BD). 当且仅当四边形内接于圆时, 等号成立.

证明

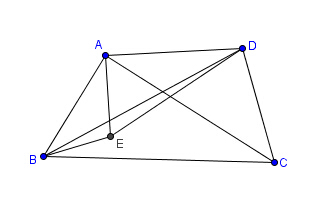
如图所示，我们找点 (E) 使得 ( riangle ABE sim riangle ACD)，利用简单题的结论有 ( riangle ABC sim riangle AED).

根据两个相似我们有

[frac{AB}{BE}=frac{AC}{CD},qquad frac{BC}{ED}=frac{AC}{AD}. ]

于是

[ABcdot CD+ADcdot BC=ACcdot(BE+ED)geq ACcdot BD. ]

另外，等号成立当且仅当 (E) 在(BD)上，这意味着(angle ABD=angle ACD), 即(ABCD)内接于圆.

一个妙用

托勒密定理是平面几何中的一个经典结论，上述证明也是常见的证明。托勒密定理有很多重要的推论，比如勾股定理、两角和的正弦公式等。下面的结论我是前几天才在matrix67的博客上看到的，非常奇妙。

任意给定自然数 (n)，我们都能在平面上找到 (n) 个点使得任意两点之间的距离都是整数个单位长度。

证明

出于便利，下文中我们将单位长度记作(1)。

• (n=3) 时，边长为 (1) 的等边三角形的三个顶点即满足条件。

• (n=4)。
  我们以长度为 (1) 的线段 (AB) 为直径作圆。我们知道，圆周上任意异于 (A), (B) 的点 (C) 都能和 (A), (B) 构成一个直角三角形，其边长满足勾股定理。 不妨取这样的点 (C)：(AC=frac{3}{5}), (BC=frac{4}{5})。我们再取这样的点 (D)：(AD=frac{5}{13}), (BD=frac{12}{13})。利用托勒密定理，我们有 (CD=frac{16}{65})。这样我们就找到了任意两点距离都是有理数的四个点。将这些距离都乘以 (65)，我们就找到了两两距离都是整数的四个点。

• (n>4)。
  在证明之前我们先回顾一个经典的数论命题

方程 (x^2+y^2=z^2) 有无限多组本原解 ((x,y,z))。 【本原解的意思是，我们将所有的((kx,ky,kz))看作一个解 ((x,y,z))。】

对于第五个点，第六个点乃至任意的 (n) 个点，我们都能通过上述方程的解将其构造出来，并保证这些点与前面的点都不相同。

无限的情形

上面的分析表明，无论你想要多少个点满足两两距离都是整数个单位长度，哪怕是一万亿个点，我们都能一步一步地将它们构造出来。那么我们把这个有限的 (n) 推到无限的情形，结果会是什么样呢？也就是说下面的命题成立吗？

我们可以在平面上找到无限多个点，使得它们两两之间的距离都是整数个单位长度。

上述命题是成立的。如果你忘掉或不知道前面的分析，你或许会反应的更快。数轴上对应于整数 (n) 的所有点即满足条件。这种情形太平凡了，我们加一个限制：这些点不分布在一条直线上，这时候上述命题还成立吗？

或许你想重复上面有限情形的论证，但很可惜，它们行不通。上述论证只能给出两两距离是有理数的点，最后对距离的数值通分，得到整数。这在无限的情形下是行不通的。那么，其他什么方法可以证明这个结论呢？事实上，没有其他方法可以证明这一点，因为加限制后的命题不成立。这就是下述定理所要说明的。

（埃尔德什）如果平面上有无限个点满足两两距离都是整数个单位长度，那么所有这些点只能分布在同一条直线上。

对于上述命题，我目前只知道一个证明，就是埃尔德什自己给出的虽然初等却非常复杂的证明。哪天有空再写一写。