[LeetCode]54. Count Primes统计素数

Description:

Count the number of prime numbers less than a non-negative number, n.

Credits:
Special thanks to @mithmatt for adding this problem and creating all test cases.

解法1：扫描一遍，依次判断每个数是否是素数，会超时 Time Limit Exceeded

class Solution {
public:
    int countPrimes(int n) {
        int cnt = 0;
        for(int i = 2; i <= n; ++i)
            if(isPrime(i)) ++cnt;
        return cnt;
    }
private:
    bool isPrime(int num) {
        for(int i = 2; i * i < num; ++i)
            if(num % i == 0) return false;
        return true;
    }
};

Hint:

1. Let's start with a isPrime function. To determine if a number is prime, we need to check if it is not divisible by any number less than n. The runtime complexity of isPrime function would be O(n) and hence counting the total prime numbers up to n would be O(n²). Could we do better?

2. As we know the number must not be divisible by any number > n / 2, we can immediately cut the total iterations half by dividing only up to n / 2. Could we still do better?

3. Let's write down all of 12's factors:

   2 × 6 = 12
   3 × 4 = 12
   4 × 3 = 12
   6 × 2 = 12
   

   As you can see, calculations of 4 × 3 and 6 × 2 are not necessary. Therefore, we only need to consider factors up to √n because, if n is divisible by some number p, then n = p × q and since p ≤ q, we could derive that p ≤ √n.

   Our total runtime has now improved to O(n^1.5), which is slightly better. Is there a faster approach?

   public int countPrimes(int n) {
      int count = 0;
      for (int i = 1; i < n; i++) {
         if (isPrime(i)) count++;
      }
      return count;
   }
   
   private boolean isPrime(int num) {
      if (num <= 1) return false;
      // Loop's ending condition is i * i <= num instead of i <= sqrt(num)
      // to avoid repeatedly calling an expensive function sqrt().
      for (int i = 2; i * i < num; i++) {
         if (num % i == 0) return false;
      }
      return true;
   }

4. The Sieve of Eratosthenes is one of the most efficient ways to find all prime numbers up to n. But don't let that name scare you, I promise that the concept is surprisingly simple.

   
   Sieve of Eratosthenes: algorithm steps for primes below 121. "Sieve of Eratosthenes Animation" by SKopp is licensed under CC BY 2.0.

   We start off with a table of n numbers. Let's look at the first number, 2. We know all multiples of 2 must not be primes, so we mark them off as non-primes. Then we look at the next number, 3. Similarly, all multiples of 3 such as 3 × 2 = 6, 3 × 3 = 9, ... must not be primes, so we mark them off as well. Now we look at the next number, 4, which was already marked off. What does this tell you? Should you mark off all multiples of 4 as well?

5. 4 is not a prime because it is divisible by 2, which means all multiples of 4 must also be divisible by 2 and were already marked off. So we can skip 4 immediately and go to the next number, 5. Now, all multiples of 5 such as 5 × 2 = 10, 5 × 3 = 15, 5 × 4 = 20, 5 × 5 = 25, ... can be marked off. There is a slight optimization here, we do not need to start from 5 × 2 = 10. Where should we start marking off?

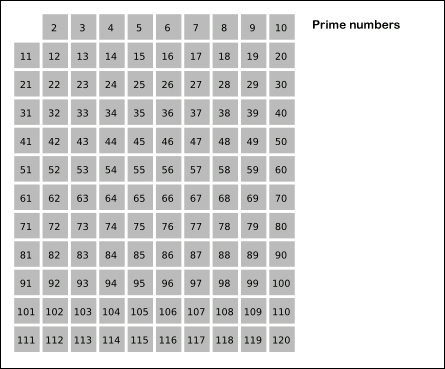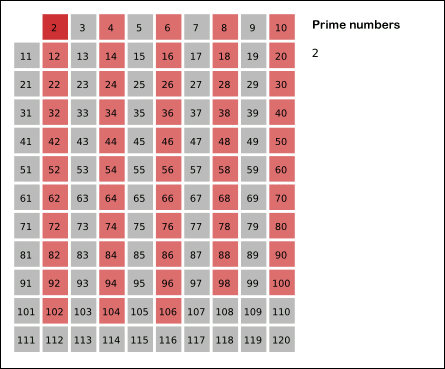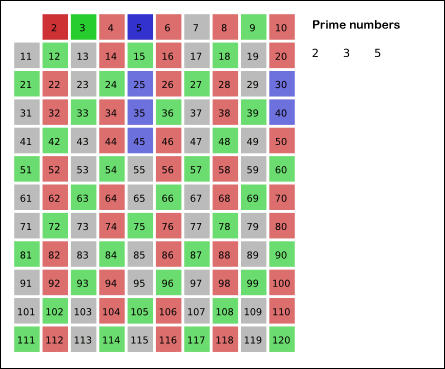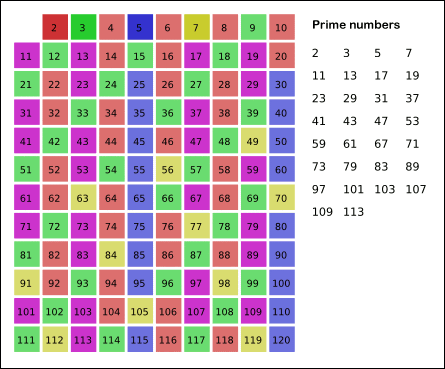
6. In fact, we can mark off multiples of 5 starting at 5 × 5 = 25, because 5 × 2 = 10 was already marked off by multiple of 2, similarly 5 × 3 = 15 was already marked off by multiple of 3. Therefore, if the current number is p, we can always mark off multiples of p starting at p², then in increments of p: p² + p, p² + 2p, ... Now what should be the terminating loop condition?

7. It is easy to say that the terminating loop condition is p < n, which is certainly correct but not efficient. Do you still remember Hint #3?

8. Yes, the terminating loop condition can be p < √n, as all non-primes ≥ √n must have already been marked off. When the loop terminates, all the numbers in the table that are non-marked are prime.

   The Sieve of Eratosthenes uses an extra O(n) memory and its runtime complexity is O(n log log n). For the more mathematically inclined readers, you can read more about its algorithm complexity on Wikipedia.

   public int countPrimes(int n) {
      boolean[] isPrime = new boolean[n];
      for (int i = 2; i < n; i++) {
         isPrime[i] = true;
      }
      // Loop's ending condition is i * i < n instead of i < sqrt(n)
      // to avoid repeatedly calling an expensive function sqrt().
      for (int i = 2; i * i < n; i++) {
         if (!isPrime[i]) continue;
         for (int j = i * i; j < n; j += i) {
            isPrime[j] = false;
         }
      }
      int count = 0;
      for (int i = 2; i < n; i++) {
         if (isPrime[i]) count++;
      }
      return count;
   }

Subscribe to see which companies asked this question

解法2：Hint的第二种解法，埃拉托斯特尼筛法。这个算法的过程如下图所示，我们从2开始遍历到根号n，先找到第一个质数2，然后将其所有的倍数全部标记出来，然后到下一个质数3，标记其所有倍数，依次类推，直到根号n，此时数组中未被标记的数字就是质数。我们需要一个n-1长度的bool型数组来记录每个数字是否被标记，长度为n-1的原因是题目说是小于n的质数个数，并不包括n。实际设计长度为n更方便。可以用bitset压缩空间。

class Solution {
public:
    int countPrimes(int n) {
        vector<int> isPrime(n, 1);
        for(int i = 2; i * i < n; ++i)
        {
            if(isPrime[i] == 1)
            {
                for(int j = i * i; j < n; j += i)
                    isPrime[j] = 0;
            }
        }
        int cnt = 0;
        for(int i = 2; i < n; ++i)
            if(isPrime[i]) ++cnt;
        return cnt;
    }
};