
欧拉函数phi的定义是:不大于它的与它互质的数的个数嘛,并且我们不加证明的给出一个性质——欧拉函数是积性函数,如果ab互质,那么phi(ab)=phi(a)phi(b)
这里代码的phi[1]=1是对1的特殊处理,然后从2开始,i枚举的是当前在判断的是数字i是不是质数
如果!vis[i] 就说明i没有被筛掉,就是质数,然后用i的倍数去筛别的数字
这里倍数的选取就是已经筛出来的质数,并且用到它的因子为止,理由已经讲过了,
就是这样才能保证每个数被其最小质因子筛掉,保证线性复杂度
这里面有两个分支
如果i%prime[j]==0,说明它是最后一个要用到的作为倍数的质数,用完它就要break,
同时,由于这里它不满足i与prime[j]互质,所以不能使用积性(如果ab互质,那么phi(ab)=phi(a)phi(b))
这里的计算用的是通项公式的展开
{
通项公式: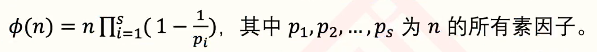
这里我们可以换元,设n后面那一坨为T,
则,φ(i*prime[j])=i*prime[j]*T
又φ(i)=i*T
所以,φ(i*prime[j])=φ(i)*prime[j]
}
然后后面的另一个分支
由于prime[j]是质数且不是i的因子,因此i和prime[j]是互质的,所以可以利用积性
phi[i*prime[j]]=phi[i] * phi[prime[j]]
因为prime[j]是质数,所以 phi[prime[j]]=prime[j]-1
这里就直接写了prime[j]-1,这样不用访问内存代码会跑得更快一些
phi[prime[j]]=prime[j]-1 是因为phi的定义:不大于它的与它互质的数的个数
就是,一个质数,比他小的所有数 都与它互质(注意正整数)
(1与任何自然数互质)