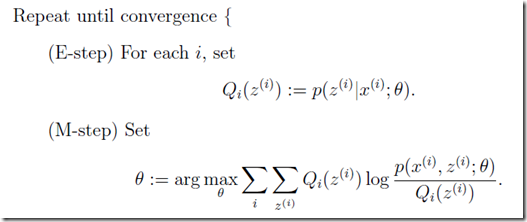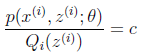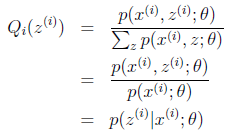K-Means聚类和EM算法复习总结

摘要：

　　1.算法概述

　　2.算法推导

　　3.算法特性及优缺点

　　4.注意事项

　　5.实现和具体例子

　　6.适用场合

内容：

1.算法概述

　　k-means算法是一种得到最广泛使用的聚类算法。 它是将各个聚类子集内的所有数据样本的均值作为该聚类的代表点。

　　k-means 计算过程：

　　（1）随机选择k个类簇的中心

　　（2）计算每一个样本点到所有类簇中心的距离，选择最小距离作为该样本的类簇

　　（3）重新计算所有类簇的中心坐标，直到达到某种停止条件（迭代次数/簇中心收敛/最小平方误差）

     期望最大化（Expectation Maximization）是在含有隐变量（latent variable）的模型下计算最大似然的一种算法

　　

其中Z是隐变量，theta是待定参数;E-step是固定参数theta,求Z的期望;M-step是theta的极大似然估计（下文会有详细推导）

扩展：k均值的其他变种（二分k均值,kmeans++,mini-batch kmeans），层次聚类，密度聚类(DBscan,密度最大值聚类)，吸引子传播算法（AP）,谱聚类，标签传递算法（LPA）

扩展：聚类的衡量指标：均一性，完整性，V-measure,轮廓系数

2.算法推导

2.1 从kmeans目标函数/损失函数角度解释其收敛性：

　　

　　从损失函数角度讲，kmeans和线性回归都是服从高斯分布的。从平方距离（L2范数球）上讲，k均值适合处理类圆形数据。

　　以上证明k均值聚类中心的梯度损失方向就是其类簇内的均值，从而从梯度下降算法/凸优化上解释了kmeans是收敛的。

2.2 使用EM算法推导K-means:

　　k-means算法是高斯混合聚类在混合成分方差相等，且每个样本仅指派一个混合成分时候的特例。k-means中每个样本所属的类就可以看成是一个隐变量，在E步中，我们固定每个类的中心，通过对每一个样本选择最近的类优化目标函数，在M步，重新更新每个类的中心点，该步骤可以通过对目标函数求导实现，最终可得新的类中心就是类中样本的均值。

2.3 EM算法的理论基础

　　期望--参见概率论杂记

　　极大似然估计--参见数理统计与参数估计杂记

　　Jensen不等式--参见凸函数与凸集杂记

2.4 EM算法的具体推导

　　先贴一个图，说明EM算法在做什么：

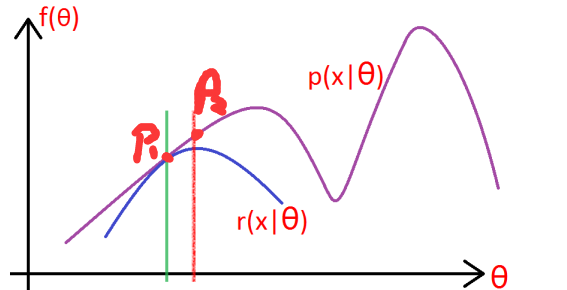
图中x是隐变量，不方便直接使用对数极大似然法求解参数thera,EM的策略就是先随便给一个条件概率p1(x1|thera)，然后找到一个l(thera)的下界函数r(x1|thera),求r的最大值p2(x2|thera)，再找到经过p2点的下界函数r2(x2|thera)，重复该过程直到收敛到局部最大值。

      给定的训练样本是，样例间独立，我们想找到每个样例隐含的类别z，能使得p(x,z)最大。

　　  

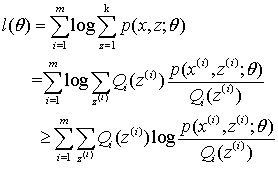
　　其中是样本i为组分z的概率，最后一步可以看作是关于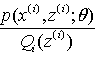的期望的凹函数的Jensen不等式

　　当不等式变成等式时，说明我们找到了最接近的函数。按照这个思路要想让等式成立，需要让随机变量变成常数值，这里得到：

      

      c为常数，不依赖于。对此式子做进一步推导，我们知道，那么也就有，那么有下式：

      

　　

在固定其他参数后，的计算公式就是后验概率，解决了如何选择的问题。这一步就是E步，建立的下界。

M步，就是在给定后，调整，去极大化的下界

 　深入：EM的收敛性证明;推导混合高斯模型

3.算法特性及优缺点

　　特性：本算法需要确定k个划分以到达平方误差最小。当聚类是密集的，且类与类之间区别明显时，效果较好。

　　优点：

　　　　（1）原理简单，实现容易；

　　　　（2）对于处理大数据集，这个算法是相对可伸缩和高效的

　　　　（3）当簇近似为高斯分布时，它的效果较好

　　缺点：

　　　　（1）在簇的平均值可被定义的情况下才能使用，可能不适用某些应用

　　　　（2）初始聚类中心的选择比较敏感，可能只能收敛到局部最优解（改进：选取距离尽可能远的点作为初始聚类 实现kmeans++）

　　　　（3）必须事先确定K的个数 （根据什么指标确定K）

　　　　（4）算法复杂度高O(nkt)

　　　　（5）不能发现非凸形状的簇，或大小差别很大的簇

 　　　  （6）对噪声和孤立点数据敏感

4.注意事项

　　k-means初值的选择：k-means是初值敏感的，可以通过根据到簇中心距离，给样本点不同的随机概率，从而避免初值敏感问题，kmeans++即此算法的实现

　　k值的选择：业务上有具体的分类数最好；如果没有，采用机器学习中的一些指标，比如损失函数最小，根据层次分类找到比较好的k值，聚类的轮廓系数等等。

　　异常点处理：去除异常点：离群值(3倍以上标准差)

      缺失值处理：特殊值填充；或者以平均值（没有数据倾斜）/中值(有数据倾斜)替换。

　　kmeans适用的场合：高斯分布

　　标准化：需要计算样本间的距离；为了避免某一维度的取值范围过大，故需要做标准化到0,1区间 

　　后处理：具有最大SSE值的簇划分为两个簇，具体实现只要将属于最大簇的数据点用K-均值聚类，设定簇数k=2即可。

　　　　　　为了保证簇总数不变，可以合并最近的质心，或者合并两个使得SSE值增幅最小的质心。

5.实现和具体例子

　　《机器学习实战》中的k-mean和二分k-means以及基于地点坐标的聚类

　　spark mllib的kmeans实现

 　　对乳腺癌数据集做聚类

　　对购物用户进行聚类并显示

　　对世界杯数据做聚类

　　混合高斯模型应用：OpenCV_基于混合高斯模型GMM的运动目标检测；语音背景音提取

　　

6.适用场合

　　支持大规模数据

　　特征维度

　　是否有 Online 算法:有，spark mllib的流式k均值

　　特征处理：支持数值型数据，类别型类型需要进行0-1编码