题意:求矩形面积并
分析:使用线段树+扫描线...因为坐标是浮点数的,因此还需要离散化!
把矩形分成两条边,上边和下边,对横轴建树,然后从下到上扫描上去,用col表示该区间有多少个下边,sum代表该区间内被覆盖的线段的长度总和
这里线段树的一个结点并非是线段的一个端点,而是该端点和下一个端点间的线段,所以题目中r+1,r-1的地方可以自己好好的琢磨一下
详细分析下扫描线
第一次完全看懂扫描线.
像这题的样例:
 这么两个矩形,现在要求它的面积并.
这么两个矩形,现在要求它的面积并.
假设我门将横边座位扫描线,即每个矩形有两条扫描线,下扫描线,下扫描线,
每条扫描线我们用结构体
const int MAXN=250; struct seg{ double x1,x2,y; int flag; bool operator <(const seg& rsh)const{ return y<rsh.y; } }G[MAXN];
来保存,保存这条扫描线的两个横坐标和一个纵坐标,还用flag标记这条扫描线是上边还是下边,下边flag=1,上边flag=-1;
将扫描线都存好后,按照横坐标排序,使得每条边从下到上的顺序(a1,a2,a3,a4)
现在可以边看程序边看这..
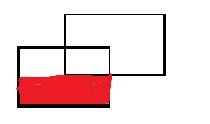
将a1插入线段树后计算a1覆盖的总长度sum[1]
则红色部分的面积就可以算出来了,sum[1]*(G[i+1].y-G[i].y)
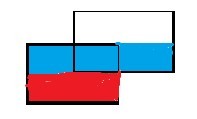
将a2插入线段树中,计算得到总长度为蓝色部分的底边,sum[1]
则蓝色部分的面积也就可以算出来了sum[1]*(G[i+1].y-G[i].y)
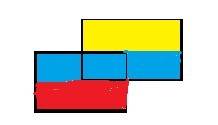
最后将a3插入树中,因为a3是上边,因此把红色的底边给消除了,这是线段树计算得的结果为黄色部分的底边sum[1]
则黄色部分的面积为sum[1]*(G[i+1].y-G[i].y)
如此,把三个部分的面积加起来就是矩形面积并了.这也就是扫描线计算计算面积并的基本过程了!
// File Name: 1151.cpp // Author: Zlbing // Created Time: 2013/7/20 14:36:01 #include<iostream> #include<string> #include<algorithm> #include<cstdlib> #include<cstdio> #include<set> #include<map> #include<vector> #include<cstring> #include<stack> #include<cmath> #include<queue> using namespace std; #define CL(x,v); memset(x,v,sizeof(x)); #define INF 0x3f3f3f3f #define LL long long #define REP(i,r,n) for(int i=r;i<=n;i++) #define RREP(i,n,r) for(int i=n;i>=r;i--) #define lson l,m,rt<<1 #define rson m+1,r,rt<<1|1 const int MAXN=250; struct seg{ double x1,x2,y; int flag; bool operator <(const seg& rsh)const{ return y<rsh.y; } }G[MAXN]; double hash[MAXN]; double sum[MAXN<<2]; int col[MAXN<<2]; void pushup(int rt,int l,int r) { if(col[rt]) { sum[rt]=hash[r+1]-hash[l]; } else if(l==r)sum[rt]=0; else sum[rt]=sum[rt<<1]+sum[rt<<1|1]; } void update(int L,int R,int flag,int l,int r,int rt) { if(L<=l&&R>=r) { col[rt]+=flag; pushup(rt,l,r); return; } int m=(l+r)>>1; if(L<=m)update(L,R,flag,lson); if(R>m)update(L,R,flag,rson); pushup(rt,l,r); } int main() { int cas=1; int n; while(~scanf("%d",&n)) { if(n==0)break; int xlen=0; double a,b,c,d; REP(i,1,n) { scanf("%lf%lf%lf%lf",&a,&b,&c,&d); G[xlen].x1=a,G[xlen].x2=c,G[xlen].y=b,G[xlen].flag=1; hash[xlen]=a; xlen++; hash[xlen]=c; G[xlen].x1=a,G[xlen].x2=c,G[xlen].y=d,G[xlen].flag=-1; xlen++; } sort(G,G+xlen); sort(hash,hash+xlen); CL(col,0); CL(sum,0); double ans=0; for(int i=0;i<xlen-1;i++) { int l=lower_bound(hash,hash+xlen,G[i].x1)-hash; int r=lower_bound(hash,hash+xlen,G[i].x2)-hash-1; if(l<=r)update(l,r,G[i].flag,0,xlen-1,1); ans+=sum[1]*(G[i+1].y-G[i].y); } printf("Test case #%d ",cas++); printf("Total explored area: %.2lf ",ans); } return 0; }