Description
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
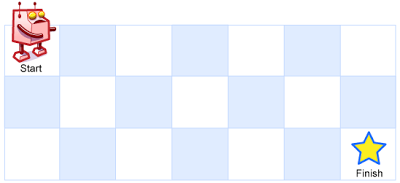
Above is a 7 x 3 grid. How many possible unique paths are there?
Note: m and n will be at most 100.
Example 1:
Input: m = 3, n = 2
Output: 3
Explanation:
From the top-left corner, there are a total of 3 ways to reach the bottom-right corner:
1. Right -> Right -> Down
2. Right -> Down -> Right
3. Down -> Right -> Right
Example 2:
Input: m = 7, n = 3
Output: 28
Analyse
有一个(m imes n)的网格,机器人处于左上方(0, 0)位置处,机器人只能向右或者向下走,计算一个机器人从(0, 0)走到(m, n)的总路线数
动态规划
dp[i][j] 代表从(0, 0)走到(i, j)的总路线数
机器人只能向右或者向下走,所以当机器人在(i, j)的时候,有两种情况
从(i-1, j)向下走了一步
从(i, j-1)向右走了一步
dp[i][j] = dp[i, j-1] + dp[i-1, j]
int uniquePaths(int m, int n) {
if (m < 0 || n < 0) return 0;
int dp[100][100];
for (int i = 0; i < m ; i++) {
dp[i][0] = 1;
}
for (int j = 0; j < n; j++) {
dp[0][j] = 1;
}
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i][j-1] + dp[i-1][j];
}
}
return dp[m-1][n-1];
}
组合数学
从(0, 0)走到(m ,n),需向右走n-1步,向下走m-1步,共 m+n-2步,路径数位(C_{m+n-2}^{m-1}) 或 (C_{m+n-2}^{n-1})
(C_m^n)的计算方法
用编程实现时可以用n控制循环次数,循环n次,依次乘上 (frac{m - i}{n - i}),i为循环变量
下面这段代码看似正确,实际上无法通过,原因是做除法的时候可能无法整除,导致计算错误
int combination(int m, int n) {
unsigned long long ans = 1;
for(int i = 0; i < n; i++) {
ans *= (m - i);
ans /= (n - i); // 此处有错误
}
return ans;
}
int uniquePaths(int m, int n) {
int a = m + n -2;
int b = min(n-1, m-1); // 利用组合的性质减少计算次数
return combination(a, b);
}
通过更换除数的顺序解决无法整除的问题, 最终代码如下
int combination(int m, int n) {
unsigned long long ans = 1;
for(int i = 0; i < n; i++) {
ans *= (m - i);
ans /= (i + 1); // 从1开始除,可以保证能够整除
}
return ans;
}
int uniquePaths(int m, int n) {
int a = m + n -2;
int b = min(n-1, m-1);
return combination(a, b);
}