宇宙,是时间和空间的总和。时间是一维的,空间。。。maybe 9 or 10维?
降维,即用一个低维度的向量表示原始高维度的特征。常见的降维方法有主成分分析、线性判别分析、等距映射、局部线性嵌入、拉普拉斯特征映射、局部保留投影等。
01 PCA最大方差理论
在机器学习领域中,我们对原始数据进行特征提取,有时会得到比较高维的特征向量。在这些向量所处的高维空间中,包含很多的冗余和噪声。我们希望通过降维的方式来寻找数据内部的特性,从而提升特征表达能力,降低训练复杂度。主成分分析(Principal Components Analysis,PCA)作为降维中最经典的方法,至今已有100多年的历史,它属于一种线性、非监督、全局的降维算法。
Q:如何定义主成分?从这种定义出发,如何设计目标函数使得降维达到提取主成分的目的?针对这个目标函数,如何对PCA问题进行求解?
A: PCA旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。举一个简单的例子,在三维空间中有一系列数据点,这些点分布在一个过原点的平面上。如果我们用自然坐标系x,y,z三个轴来表示数据,就需要使用三个维度。而实际上,这些点只出现在一个二维平面上,如果我们通过坐标系旋转变换使得数据所在平面与x,y平面重合,那么我们就可以通过x′,y′两个维度表达原始数据,并且没有任何损失,这样就完成了数据的降维。而x′,y′两个轴所包含的信息就是我们要找到的主成分。
但在高维空间中,我们往往不能像刚才这样直观地想象出数据的分布形式,也就更难精确地找到主成分对应的轴是哪些。不妨,我们先从最简单的二维数据来看看PCA究竟是如何工作的,如图4.1所示。
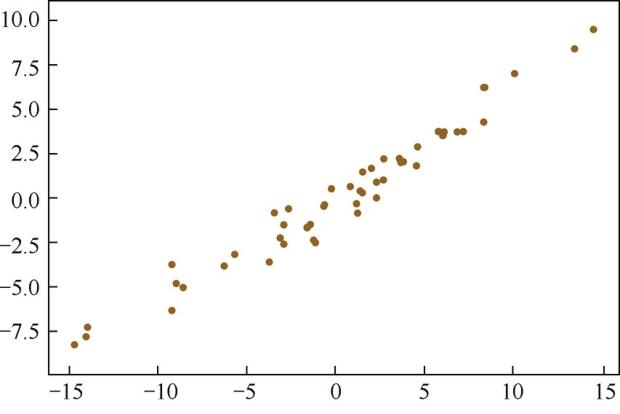
(a)二维空间中经过中心化的一组数据
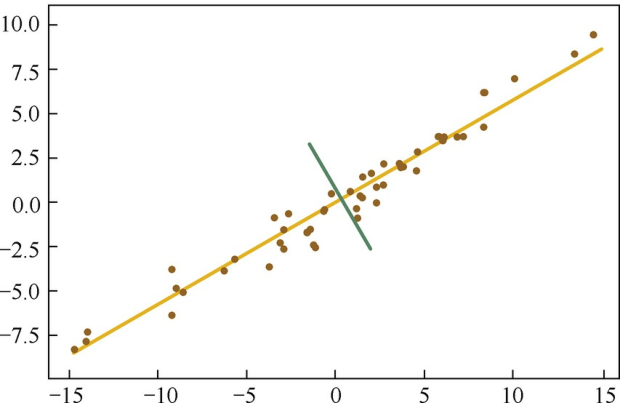
(b)该组数据的主成分
图4.1 二维空间数据主成分的直观可视化
图4.1(a)是二维空间中经过中心化的一组数据,我们很容易看出主成分所在的轴(以下称为主轴)的大致方向,即图4.1(b)中黄线所处的轴。因为在黄线所处的轴上,数据分布得更为分散,这也意味着数据在这个方向上方差更大。在信号处理领域,我们认为信号具有较大方差,噪声具有较小方差,信号与噪声之比称为信噪比。信噪比越大意味着数据的质量越好,反之,信噪比越小意味着数据的质量越差。由此我们不难引出PCA的目标,即最大化投影方差,也就是让数据在主轴上投影的方差最大。
02 PCA最小平方误差理论
上一节介绍了从最大方差的角度解释PCA的原理、目标函数和求解方法。本节将通过最小平方误差的思路对PCA进行推导。
Q:PCA求解的其实是最佳投影方向,即一条直线,这与数学中线性回归问题的目标不谋而合,能否从回归的角度定义PCA的目标并相应的求解问题呢?
A:看书吧
03 线性判别分析
线性判别分析(Linear Discriminant Analysis,LDA)是一种有监督学习算法,同时经常被用来对数据进行降维。
相比于PCA,LDA可以作为一种有监督的降维算法。在PCA中,算法没有考虑数据的标签(类别),只是把原数据映射到一些方差比较大的方向上而已。
假设用不同的颜色标注C 1 、C 2 两个不同类别的数据,如图4.4所示。根据PCA算法,数据应该映射到方差最大的那个方向,亦即y轴方向。但是,C 1 ,C 2 两个不同类别的数据就会完全混合在一起,很难区分开。所以,使用PCA算法进行降维后再进行分类的效果会非常差。但是,如果使用LDA算法,数据会映射到x轴方向。那么,LDA算法究竟是如何做到这一点的呢?
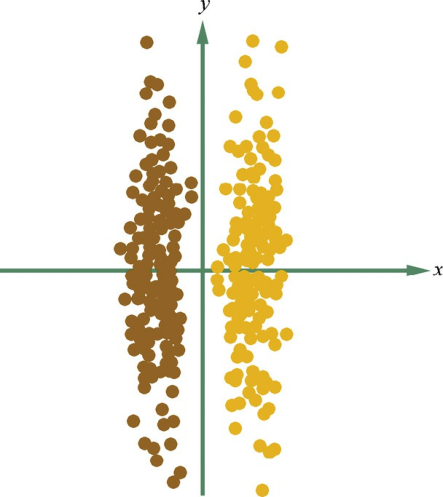
Q:对于具有类别标签的数据,应当如何设计目标函数使得降维的过程中不损失类别信息?在这种目标下,应当如何进行求解?
A:
LDA首先是为了分类服务的,因此只要找到一个投影方向ω,使得投影后的样本尽可能按照原始类别分开。
04 线性判别分析与主成分分析
同样作为线性降维方法,PCA是有监督的降维算法,而LDA是无监督的降维算法。虽然在原理或应用方面二者有一定的区别,但是从这两种方法的数学本质出发,我们不难发现二者有很多共通的特性。
Q:LDA和PCA作为经典的降维算法,如何从应用的角度分析其原理的异同?从数学推导的角度,两种降维算法在目标函数上有何区别与联系?
A:看书看书