题目大意:有n个按钮排成一条直线,你的任务是通过左右移动按下所有按钮,按钮如果一段时间没有被按下就会被弹开。
以下是我的推论(不一定正确):
直观地看的话,如果选择的是最优路径,那么路径的形状必然是若干条区域逐渐缩小的折线,如图所示:
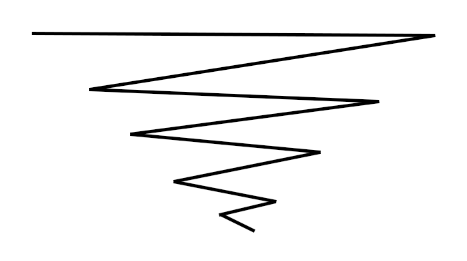
而不可能出现这个样子:

因为,如果这样走的话,那么中间从A到B一段反复经过的区域就全都浪费了,不如直接从C走到D划算。
进一步观察可以发现,每一个按钮只有最后一次被按下的时候是有效的,因此答案序列应当是一个从两边向中间聚合的过程。
设dp[L][R][f]表示当前在区间[L,R]的左端点(f=0)或右端点(f=1),将区间[L,R]中的所有按钮全部按下所需的最短时间,每一步只有两种选择:
1.按下当前按钮并往前走一步,以后就都不管这个按钮了,此时$dp[L][R][0]=min(dp[L][R][0],dp[L+1][R][0])+dis[L+1]-dis[L]) $(以左端点为例,右端点类似,下同。dis[i]表示i点与左端点的距离)
2.跑到对面去准备按下对面的按钮,此时$dp[L][R][0]=min(dp[L][R][0],dp[L][R][1])+dis[R]-dis[L]) $
总复杂度$O(n^2)$
吐槽:ZOJ凉了,HDU后台有问题过不了,只能交到UVAlive上了,QAQ
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N=200+10,inf=0x3f3f3f3f; 5 int dp[N][N][2],op[N][N][2],n,t[N],dis[N]; 6 int dfs(int L,int R,int f) { 7 int& ret=dp[L][R][f],&opp=op[L][R][f]; 8 if(~ret)return ret; 9 if(L==R)return ret=0; 10 ret=inf; 11 if(f==0) { 12 int x=dfs(L+1,R,0)+dis[L+1]-dis[L]; 13 int y=dfs(L,R,1)+dis[R]-dis[L]; 14 if(x<t[L]&&x<ret)ret=x,opp=0; 15 if(y<ret)ret=y,opp=1; 16 } else { 17 int x=dfs(L,R-1,1)+dis[R]-dis[R-1]; 18 int y=dfs(L,R,0)+dis[R]-dis[L]; 19 if(x<t[R]&&x<ret)ret=x,opp=0; 20 if(y<ret)ret=y,opp=1; 21 } 22 return ret; 23 } 24 vector<int> ans; 25 void pr(int L,int R,int f) { 26 if(L==R) {ans.push_back(L); return;} 27 int opp=op[L][R][f]; 28 if(opp==0) { 29 if(f==0)ans.push_back(L),pr(L+1,R,f); 30 else ans.push_back(R),pr(L,R-1,f); 31 } else pr(L,R,f^1); 32 } 33 int main() { 34 while(scanf("%d",&n)==1) { 35 for(int i=1; i<=n; ++i)scanf("%d",&t[i]); 36 for(int i=1; i<=n; ++i)scanf("%d",&dis[i]); 37 memset(dp,-1,sizeof dp); 38 int x=dfs(1,n,0),y=dfs(1,n,1); 39 if(x==inf&&y==inf)puts("Mission Impossible"); 40 else { 41 ans.clear(); 42 if(x<=y)pr(1,n,0); 43 else pr(1,n,1); 44 for(int i=0; i<ans.size(); ++i)printf("%d%c",ans[i]," "[i==ans.size()-1]); 45 } 46 } 47 return 0; 48 }