Motion-Based Calibration of Multimodal Sensor Arrays
多模态传感器阵列的基于运动的标定
背景:
传感器对准需要高精度,传感器也具有外壳,物理测量传感器的相对位置不切实际。有些环境运行一段时间后,校准精度会下降。为了实现自动,因此需要实现自动标定,动态更新校准参数。
传统标定方法:传统的标定方法,需要在环境中手动放置markers或者在传感器的输出中,手动标出控制点,缺点是慢,效率不高,需要有一定的标定经验。
一些自动标定方法的局限性:受限于单一的传感器,取决于用户给的初始化质量,完全依赖外部感知数据的方法需要重叠的视野。
优点:
原来的标定复杂的原因:外部校准方法要么基于特殊的标记和/或棋盘,要么需要精确的参数初始化以使校准收敛。这两个限制使它们无法完全自动化。消除了对特殊标记的需要,
也消除了对手动初始化的需要。
第三个优点是基于运动的自动初始化不需要传感器之间重叠的视场。本文还提供了一种估计校准结果准确度的方法。
我们论文的主要贡献是:
一种基于运动的校准方法,它利用了所有传感器的运动及其相关的不确定性。
使用基于运动的初始化来约束现有的激光雷达摄像机技术。
引入了一种新的基于运动的激光雷达摄像机标定方法。
给出最终系统不确定性估计值的校准方法。
在两个不同平台的两个不同环境中进行评估。
手眼标定方法:
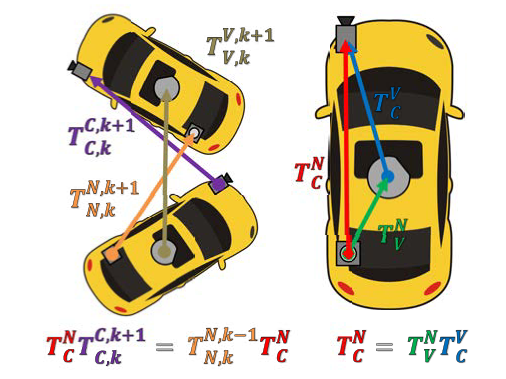
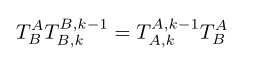

考虑定时偏移:由于典型的传感器阵列可以由一系列异步运行的传感器组成,因此出现读数的时间可能会显著不同[17]。为了说明这一点,在更新速度最慢的传感器获得读数时,
对传感器的每个变换进行插值。对于平移,使用线性插值;对于旋转,使用Slerp(球面线性插值)。


方法:
求旋转:
Kabsch算法是一种计算两个向量之间旋转矩阵的方法,提供最小的最小平方误差。使用的Kabsch算法经过了修改,为每个传感器读数提供了非相等的权重。分配给每个时间步读数的权重由等式4给出
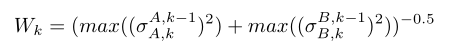
其中σ2是方差。取最大值使方差独立于旋转,并允许将其减少为单个数字。
剔除异常点,通过标准差。
初始估计用于形成旋转矩阵,给出任意两个传感器之间的旋转。使用此旋转矩阵,传感器的方差为5。这用于查找一对传感器的误差,如等式6所示。
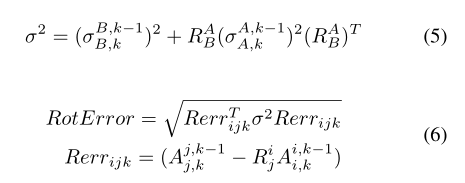
所有传感器对的误差组合在一起,形成系统的单一误差度量。使用梯度下降优化程序(在我们的实现中为Nelder-Mead单纯形)将该误差降至最低,以找到最佳旋转角度。
求平移:
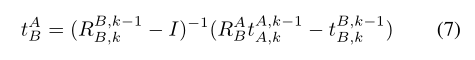
这些项可以重新排列,并与来自其他时间步的信息相结合,得到等式8
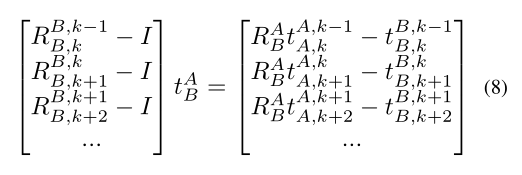
只有 tAB 未知,平移估计在很大程度上取决于旋转矩阵估计的精度,并且是对噪声最敏感的参数。
 在地面平台上,趋近于0
在地面平台上,趋近于0
优化平移:要优化的最终成本函数是所有传感器组合的等式9之和,旋转也是如此。
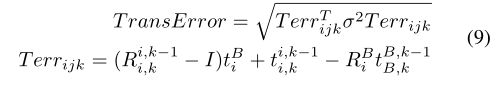
计算总方差
为了找到系统的总体差异,传感器转换将自举,粗略优化将重新运行100次。Bootstrapping用于估计方差,因为它自然地考虑了一些非线性关系,例如估计的平移依赖于旋转精度
细化传感器间转换
我们的方法引入的一个关键好处是消除了基于外部观察的校准方法所需的初始化限制。
结合细化结果