树状数组支持的最基本的操作:修改一个点的值,查询区间的值。
如果我们用最入门的暴力方法,修改点值复杂度为O(1),查询区间值复杂度是O(n);如果在加上前缀和的思想的话,查询区间变为O(1),但是修改点的值的话就变成了O(n)了。而树状数组运用的是二进制的思想,也就是说,他可以把查询时间和修改时间平摊为O(logn)。比如说储存7的话,把7拆成1+2+4(2^0+2^1+2^2,因为7=111(2)),也就是说,查询a[7]的值的话需要累加c[1],c[2],c[4](c就是树状数组)。
对于树状数组,其实就是一个数组c,只不过是树形状的,而c[i]=sum(a[j]),i-lowbit(i)+1<=j<=i。lowbit(i)就是把i变成二进制后取最右边的第一个1,如同lowbit(7)=lowbit(111)=1;lowbit的快速实现方法:lowbit(i)=i&(-i);
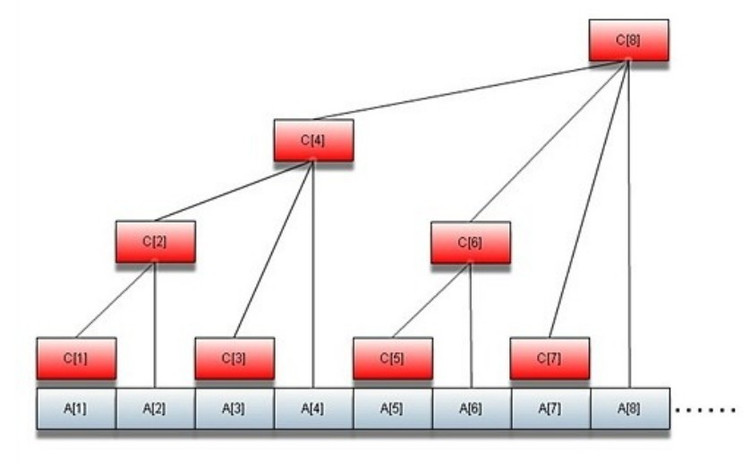
我们很明显的可以发现,如果你要修改a3的值的话,我们需要一直往上修改直到接线。
同时,查找操作的话在最开头就已经分析过了,就是sum(c[i],c[i-lowbit(i)],c[i-lowbit(i)-lowbit(i-lowbit(i))]…)
修改代码如下:
void add(int i,int val)//i是这个数的下标,val是修改的值 { while(i<=n) { c[i]+=val; i+=lowbit(i); } }
查询区间和的操作如下:
int sum(int i) { int num=0; while(i>0) { num+=c[i]; i-=lowbit(i); } return num; }
这就是树状数组最简单的入门了。
注意:树状数组的下标必须从1开始,,因为lowbit(0)=0,如果从0开始的话就会陷入死循环!!树状数组适用于所有满足结合律的运算(加法,乘法,异或等)
所有树状数组能完成的操作线段树都能够完成,但是线段树的代码复杂,时间复杂度也比较高,查询、修改需要递归完成,而,树状数组的操作不仅代码简洁,便于理解,而且一切都是递推完成的,所以能用树状数组解决的问题尽量不要用线段树来写。
这就是树状数组最简单的操作了,当然树状数组的功能不止这一些,他还可以扩展到二维,可以查找逆序对,对于LIS问题可以查找方案数,而且如果只进行区间的修改和单点的查询,树状数组也可以完成,但是这里就不做叙述了。