实验说明
数据结构实验三 二叉树的实验——二叉树的主要遍历算法
一、实验目的
通过本实验使学生熟悉二叉树遍历的各种算法;掌握采用递归实现二叉树遍历算法的方法;深刻理解栈在递归中的作用,进而学会递归转为非递归的方法;特别训练学生在编程上控制复杂结构的能力,为今后控制更为复杂结构,进而解决有一定难度的复杂问题奠定基础。
二、实验内容
1.编程实现前、中、后序的递归与非递归算法(共六个算法)。特别要求:设计并实现构造二叉树链式存储的算法。
2.进一步提供如下算法:
(1)设计与实现层序遍历的递归与非递归算法;
(2)提供另一种构造二叉树链式存储的算法;
(3)提供另外一种后序非递归遍历的实现算法。
实验报告
1.实现功能描述
编程实现前、中、后序的递归与非递归算法(共六个算法)。特别要求:设计并实现构造二叉树链式存储的算法。
2.方案比较与选择
(1)可以使用栈和队列来实现非递归算法。因为栈的功能足以完成题目要求,所以使用栈来实现。
3.设计算法描述
(1)定义一个结构体代表结点,其中包含数据域data和左右孩子。
(2)设计栈。
(3)进行模块划分,给出功能组成框图。形式如下:

(4)基本功能模块:
①前序创建并输入二叉树
②前序遍历二叉树
③中序遍历二叉树
④后序遍历二叉树
(5)用流程图描述关键算法:
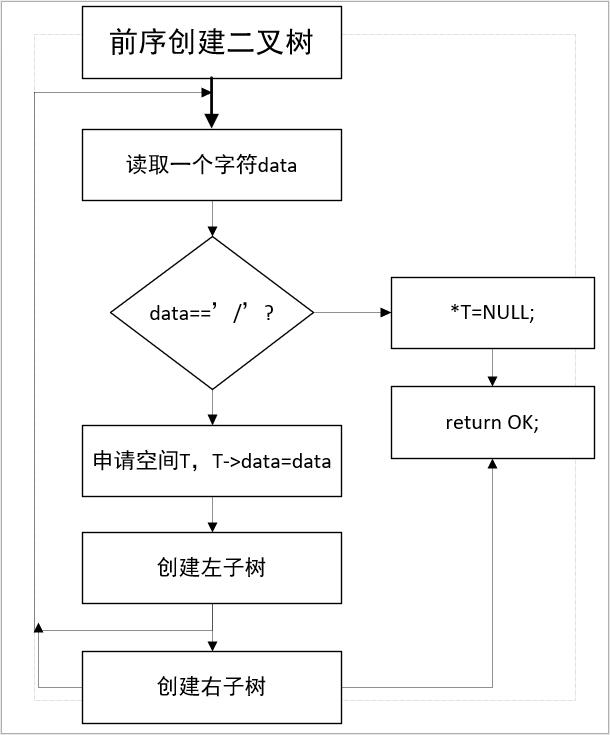
4.算法实现(即完整源程序,带注解)
(1)递归算法:
点击查看详细内容
/*
编程实现前、中、后序的递归与非递归算法(共六个算法)。
特别要求:设计并实现构造二叉树链式存储的算法。
ABDH//I///CF/K//G//
AB/EJ///CF/M//G//
*/
#include<stdio.h>
#include<stdlib.h>
#define ERR 1
#define OK 0
typedef struct BTNode {
char data;
struct BTNode* lchild, * rchild;
}BTNode, * BT;
int CreateBT(BT* T);
int PreOrderTraverse(BT T);
int InOrderTraverse(BT T);
int PostOrderTraverse(BT T);
int main(void) {
BT bt = NULL;
printf("请按前序输入二叉树(输入/代表空):");
CreateBT(&bt);
printf("
二叉树前序遍历:");
PreOrderTraverse(bt);
printf("
二叉树中序遍历:");
InOrderTraverse(bt);
printf("
二叉树后序遍历:");
PostOrderTraverse(bt);
return OK;
}
//前序创建二叉树
int CreateBT(BT* T) {
char data;
scanf("%c", &data);
if (data == '/') *T = NULL;
else {
*T = (BT)malloc(sizeof(BTNode));
if (!*T) {
printf("error:CreateBT");
return ERR;
}
(*T)->data = data;
CreateBT(&(*T)->lchild);
CreateBT(&(*T)->rchild);
}
return OK;
}
//二叉树前序遍历
int PreOrderTraverse(BT T) {
if (T != NULL) {
printf("%c ", T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
return OK;
}
//二叉树中序遍历
int InOrderTraverse(BT T) {
if (T != NULL) {
InOrderTraverse(T->lchild);
printf("%c ", T->data);
InOrderTraverse(T->rchild);
}
return OK;
}
//二叉树后序遍历
int PostOrderTraverse(BT T) {
if (T != NULL) {
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c ", T->data);
}
return OK;
}
(2)非递归算法:
点击查看详细内容
/*
编程实现前、中、后序的递归与非递归算法(共六个算法)。
特别要求:设计并实现构造二叉树链式存储的算法。
ABDH//I///CF/K//G//
AB/EJ///CF/M//G//
*/
#include<stdio.h>
#include<stdlib.h>
#define ERR 1
#define OK 0
typedef struct BTNode {
char data;
struct BTNode* lchild, * rchild;
} BTNode;
typedef struct Stack {
BTNode* bt;
int top;
int base;
int stacksize;
} Stack;
BTNode* CreatBT(BTNode* BT);
void InOrderTraverse(BTNode* BT);
void PreOrderTraverse(BTNode* BT);
void PostOrderTraverse(BTNode* BT);
void InitStack(Stack* S);
void GetTop(Stack S, BTNode* e);
void Pop(Stack* S, BTNode* e);
void Push(Stack* S, BTNode e);
int StackEmpty(Stack* S);
int main(void) {
BTNode* BT = NULL;
printf("请按前序输入二叉树(输入/代表空):");
BT = CreatBT(BT);
printf("
二叉树前序遍历:");
PreOrderTraverse(BT);
printf("
二叉树中序遍历:");
InOrderTraverse(BT);
printf("
二叉树后序遍历:");
PostOrderTraverse(BT);
return OK;
}
//前序创建二叉树
BTNode* CreatBT(BTNode* BT) {
char data;
scanf("%c", &data);
if (data == '/') BT = NULL;
else {
BT = (BTNode*)malloc(sizeof(BTNode));
BT->data = data;
BT->lchild = CreatBT(BT->lchild);
BT->rchild = CreatBT(BT->rchild);
}
return BT;
}
//二叉树前序遍历
void PreOrderTraverse(BTNode* BT) {
BTNode* bt = BT;
Stack S;
InitStack(&S);
do {
while (bt != NULL) {
printf("%c ", bt->data);
Push(&S, *bt);
bt = bt->lchild;
}
if (S.top != 0) {
bt = (BTNode*)malloc(sizeof(BTNode));
Pop(&S, bt);
bt = bt->rchild;
}
} while (!StackEmpty(&S) || (bt != NULL));
}
//二叉树中序遍历
void InOrderTraverse(BTNode* BT) {
BTNode* bt = BT;
Stack S;
InitStack(&S);
while (bt || !StackEmpty(&S)) {
if (bt) {
Push(&S, *bt);
bt = bt->lchild;
}
else {
bt = (BTNode*)malloc(sizeof(BTNode));
Pop(&S, bt);
printf("%c ", bt->data);
bt = bt->rchild;
}
}
}
//二叉树后序遍历
void PostOrderTraverse(BTNode* BT){
BTNode* bt = BT;
//用于存储上个已使用过的结点
BTNode* lastnode = BT;
Stack S;
InitStack(&S);
while (bt || !StackEmpty(&S)) {
if (bt) {
Push(&S, *bt);
bt = bt->lchild;
}
else {
bt = (BTNode*)malloc(sizeof(BTNode));
Pop(&S, bt);
if (bt->rchild && bt->rchild->data != lastnode->data) {
Push(&S, *bt);
bt = bt->rchild;
Push(&S, *bt);
bt = bt->lchild;
}
//右子树为空或者右子树已经被访问
else {
printf("%c ", bt->data);
//lastnode储存结点
lastnode = bt;
bt = NULL;
}
}
}
}
//栈的初始化
void InitStack(Stack* S) {
S->bt = (BTNode*)malloc(sizeof(BTNode) * 100);
S->top = 0;
S->base = 0;
S->stacksize = 100;
}
//获取栈顶元素
void GetTop(Stack S, BTNode* e) {
if (S.top == S.base) {
return;
}
*e = S.bt[S.top];
}
//弹栈
void Pop(Stack* S, BTNode* e) {
if (S->top == S->base) {
return;
}
*e = S->bt[--S->top];
}
//压栈
void Push(Stack* S, BTNode e) {
//如果栈满
if (S->top - S->base >= S->stacksize) {
return;
}
S->bt[S->top++] = e;
}
//判断栈是否为空
int StackEmpty(Stack* S) {
if (S->top == S->base) {
return ERR;
}
else {
return OK;
}
}
5.实验结果测试与分析
(1)数据测试程序截图
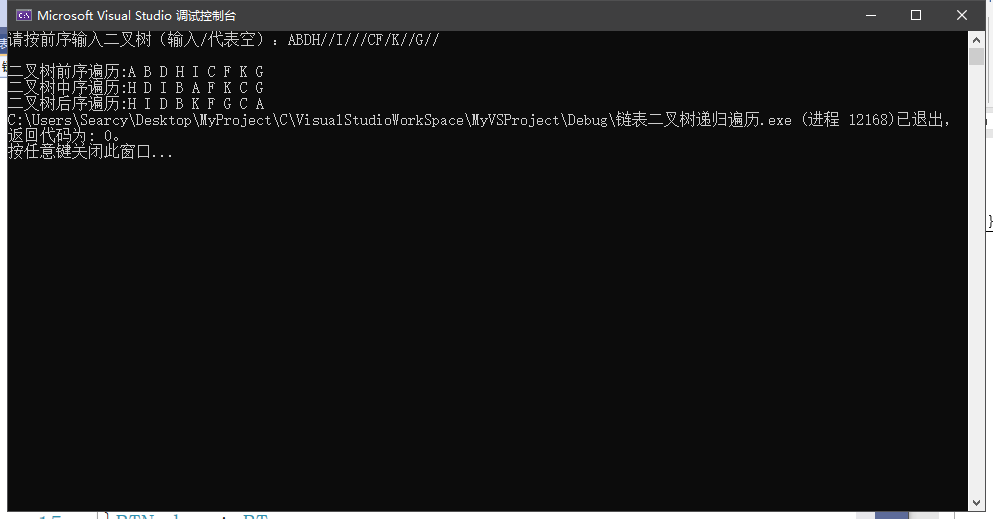
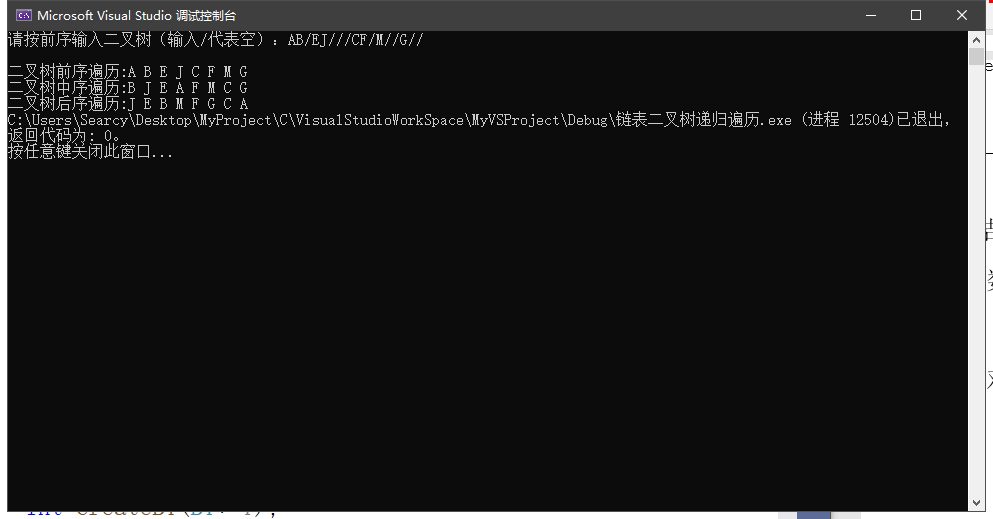
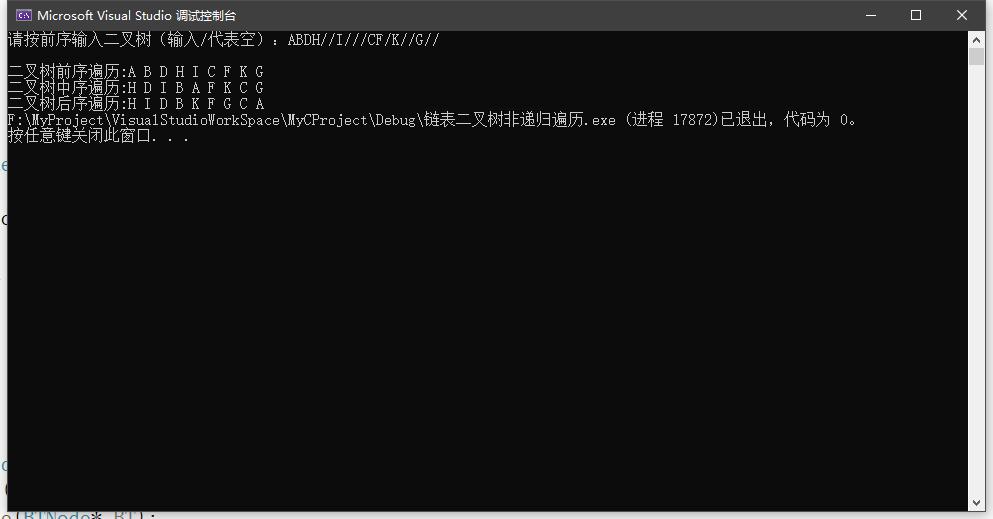
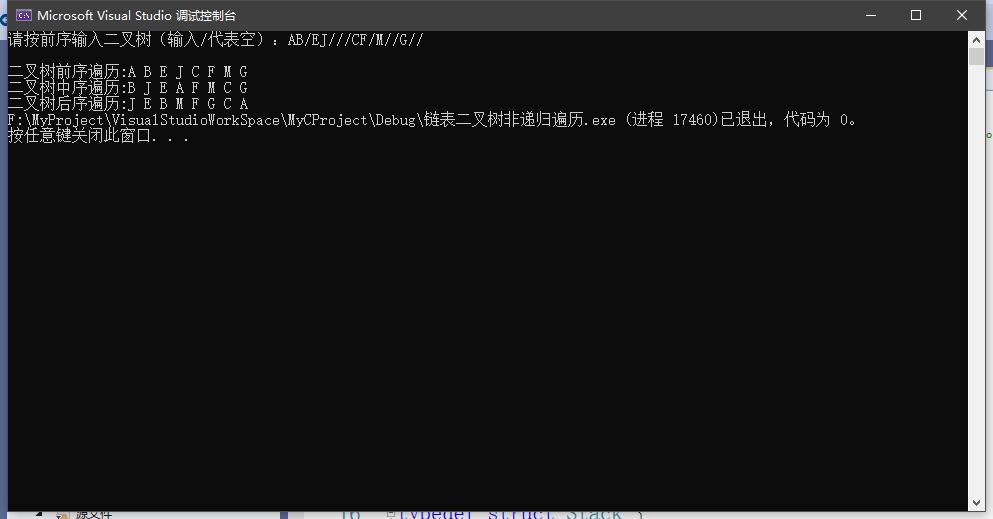
(2)对结果进行分析:
①前序遍历正确
②中序遍历正确
③后序遍历正确
④栈运行正常
6.思考及学习心得
(1)描述实验过程中对此部分知识的认识:
(2)特别描述在学习方法上的收获及体会;
(3)针对前面的思考题内容在此回答。
1)实现了简单的栈,更进一步理解和掌握栈的的使用。
2)这次的实验,巩固了我的编程模块化的思想。模块化降低了程序的耦合性,提高了程序的内聚性;降低了程序复杂度,使程序设计、调试和维护等操作简单化。模块化使得程序设计更加简单和直观,从而提高了程序的易读性和可维护性,而且还可以把程序中经常用到的一些计算或操作编写成通用函数,以供随时调用。
3)尝试在顺序存储结构上设计这些遍历算法,并在时空效率上与链式存储进行分析对比,并得出结论(仅是分析得出结论即可,可以不实现):链表法时间复杂度较高,空间复杂度较低;数组法时间复杂度较低,空间复杂度较高。因为数组法一开始就定义好树的大小,如果有空节点就浪费了空间,而链表法不会创建空结点,因此数组法的空间复杂度较高。链表法对指针的操作较繁琐,所需时间长,因此链表法的时间复杂度较低。