2.4.1 线段树

1.线段树的概念：

　　线段树是擅长处理区间的，形如下图的数据结构。线段树是一颗完美二叉树（Perfect Binary Tree）,树上的每个节点都维护一个区间。根维护的是整个区间，每个节点维护的是父亲的区间二等分后的其中一个子区间。当有n个元素时，对区间的操作可以在O（log n）的时间内完成。

                                                                    

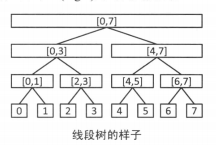
根据节点中维护的数据的不同，线段树可以提供不同的功能。下面我们以实现了Range Minimum Query（RMQ）操作的线段树为例进行说明。

2.基于线段树的RMQ的结构

下面要建立的线段树在给定数列a0,a1,……,a(n-1)的情况下，可以在O（log n）时间内完成如下两种操作：

（1）给定s和t，求a（s），a（s+1），……，a（t）的最小值

（2）给定 i 和 x，把 ai 的值改成x

如下图，线段树的每个节点维护对应区间的最小值。在建树时，只需要按从下到上的顺序分别取左右儿子的值中较小者就可以了。

                                         

3.基于线段树的RMQ的查询

如果要求a0，……，a6的最小值。我们只需要求下图中的三个节点的值的最小值即可。

                                           

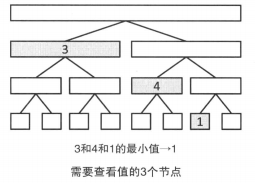
像这样，即使查询的是一个比较大的区间，由于较靠上的节点对应较大的区间，通过这些区间就可以知道大部分值的最小值，从而只需访问很少的节点就可以求得最小值。

要求某个区间的最小值，像下面这样递归处理就可以了。

　　如果所查询的区间和当前节点对应的区间完全没有交集，那么就返回一个不影响答案的值（例如INT—MAX）。

　　如果所查询的区间完全包含了当前节点对应的区间，那么就返回当前节点的值。

　　以上两种情况都不满足的话，就对两个儿子递归处理，返回两个结果中的较小者。

4.基于线段树的RMQ的值的更新

在更新a0的值时，需要重新计算下图所示的4个节点的值。

                                                          

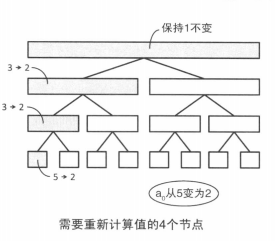
在更新ai的值时，需要对包含 i 的所有区间对应的节点的值重新进行计算。在更新时，可以从下面的节点开始向上不断更新，把每个节点的值更新为左右两个儿子的值的较小者就可以了。

5.基于线段树的RMQ的复杂度

不论哪种操作，对于每个深度都最多访问常数个节点。因此对于n个元素，每一次操作的复杂度是O（log n）。对于二叉搜索树，我们曾经提到过可能有因操作不当而导致退化的情况发生，从而使复杂度变得很糟糕。不过因为线段树不会添加或删除节点，所以即使是朴素的实现也都能在O（log n）时间内进行各种操作。

此外，n个元素的线段树的初始化的时间复杂度和总的空间复杂度都是O（n）。这是因为节点数是

n+n/2+n/4+……=2n。直觉上很容易让人产生复杂度是O（n log n）的错觉，需要注意。

6.基于线段树的RMQ的实现

为了简单起见，在建立线段树时，把数列所以的值都初始化为INT—MAX。此外，query的参数中不止传入节点的编号，还传入了节点对应的区间。

虽然从节点的编号也可以计算出对应的区间。但是把区间作为参数传入就可以节省这一步计算，为了简单起见，我们在实现中传入了对应的区间。

    #include<iostream>
    using namespace std;
    const int MAX_N = 1 << 17;
    int n, dat[2 * MAX_N - 1];
    int MAX = 100000;
    void init(int m){
      n = 1;
      while(n < m) n *= 2;
      for(int i = 0; i < 2*n-1; i++)
        dat[i] = MAX;
    }
    void update(int k, int a){
      k += n-1;
      dat[k] = a;
      while(k > 0){
        k = (k - 1) / 2;
        dat[k] = min(dat[k*2+1], dat[k*2+2]);
      }
      /*cout<<k<<" "<<a<<" "<<n <<endl;
      for(int i=0;i<15;i++)
          cout<<dat[i]<<" ";
        cout<<endl;*/
    }
    int query(int a, int b, int k, int l, int r){
      if(r <= a || b <= l) return MAX;
      if(a <= l && r <= b) return dat[k];
      else{
        int vl = query(a, b, k*2+1, l , (l+r)/2);
        int vr = query(a, b, k*2+2, (l+r)/2, r);
        //cout<<"vl= "<<vl<<" vr= "<<vr<<endl;
        return min(vl,vr);
      }
    }
    int main(){
      int y = 8;
      init(y);
      for(int i = 0; i < y; i++){
        int x;
        cin>>x;
        update(i,x);
      }
      //update(0,9);
      /*for(int i = 0; i < 15; i++)
        cout<<dat[i]<<" ";
      cout<<endl;*/
      int m=query(0, y, 0, 0, y);
      cout<<m<<endl;
      getchar();
      return 0;
    }
    //0 1 2 3 4 5 6 7
    //1 2 3

模板：

#include<iostream>
using namespace std;

struct Node{
    int l;
    int r;
    int maxvalue;
    int sum;
    int add;
}; 

Node a[100000];

// 初始化 区间[left, right]， k：当前线段树位置 
void init(int left, int right, int k) {
    a[k].l = left;
    a[k].r = right;
    a[k].maxvalue = 0;
    a[k].sum = 0;
    a[k].add = 0;
    
    if (left != right) {
        int mid = (left + right) / 2;
        init(left, mid, 2 * k);
        init(mid + 1, right, 2 * k + 1);
    }
}

// 单点更新 i：当前线段树位置， k：目标位置 ， value：更新值 
void update(int i, int k, int value) {
    if (a[i].l  == a[i].r ) {
        a[i].maxvalue = value;
        a[i].sum = value;
        return;
    }
    
    int mid = (a[i].l + a[i].r ) / 2;
    if (k <= mid) update(2 * i, k, value);
    else update(2 * i + 1, k, value);
    
    a[i].maxvalue = max(a[2 * i].maxvalue , a[2 * i + 1].maxvalue );
    a[i].sum = a[2 * i].sum + a[2 * i + 1].sum ;
}

//区间更新 i:当前位置,  更新区间[x, y], k: 区间同时操作值 
void update_add(int i, int x, int y, int k) {
    if (x == a[i].l  && y == a[i].r  ) {
        a[i].add += (y - x + 1) * k;
        return;
    }
    int mid = (a[i].l + a[i].r ) / 2;
    if(y <= mid) update_add(2 * i , x, mid, k);
    else if(x > mid) update_add(2 * i + 1, mid + 1, y, k);
    else {
        update_add(2 * i, x, mid, k);
        update_add(2 * i + 1, mid + 1, y, k);
    }
}

// 区间和 i:当前线段树位置， 查询区间[x, y] 
int query_sum(int i, int x, int y){
    if (x == a[i].l  && y == a[i].r )
        return a[i].sum  + a[i].add ;
        
    int mid = (a[i].l + a[i].r ) / 2;
    if (y <= mid) return query_sum(2 * i, x, y);
    else if (x > mid) return query_sum(2 * i + 1, x, y);
    else return query_sum(2 * i, x, mid) + query_sum(2 * i + 1, mid + 1, y);    
}

// 最大值  i：当前线段树位置， 查询区间[x, y]; 
int query_max(int i, int x, int y) {
    if (x == a[i].l && y == a[i].r ) return a[i].maxvalue ;
    
    int mid = (a[i].l + a[i].r ) / 2;
    if (y <= mid) return query_max(2 * i, x, y);
    else if (x > mid) return query_max(2 * i + 1, x, y);
    else return max (query_max(2 * i, x, mid), query_max(2 * i + 1, mid + 1, y));
}

int main() {
    int n, m;
    cin >> n >> m;
    init(1, n, 1);
    
    for (int i = 1; i <= n; i++) {
        int value;
        cin >> value;
        update(1, i, value);
    }
    
    //update_add(1, 1, 4, 1);
    //for (int i = 0; i < 10; i++) 
    //    printf("left: %d right: %d maxvalue: %d sum: %d add: %d
", a[i].l , a[i].r , a[i].maxvalue , a[i].sum , a[i].add );
    
    
    for (int i = 0; i < m; i++) {
        int op, x, y;
        cin >> op >> x >> y;
        if(op == 1) update(1, x, y);
        if(op == 2) cout << query_max(1, x, y) << endl;
        if(op == 3) cout << query_sum(1, x, y) << endl;
    }
    return 0;
}

7.需要运用线段树的问题

ALGO-8. 操作格⼦（线段树）
问题描述
有n个格⼦，从左到右放成⼀排，编号为1-n。
共有m次操作，有3种操作类型：
1.修改⼀个格⼦的权值，
2.求连续⼀段格⼦权值和，
3.求连续⼀段格⼦的最⼤值。
对于每个2、3操作输出你所求出的结果。
输⼊格式
第⼀⾏2个整数n，m。
接下来⼀⾏n个整数表示n个格⼦的初始权值。
接下来m⾏，每⾏3个整数p,x,y，p表示操作类型，p=1时表示修改格⼦x的权值为y，p=2时表示求区
间[x,y]内格⼦权值和，p=3时表示求区间[x,y]内格⼦最⼤的权值。
输出格式
有若⼲⾏，⾏数等于p=2或3的操作总数。
每⾏1个整数，对应了每个p=2或3操作的结果。
样例输⼊
4 3
1 2 3 4
2 1 3
1 4 3
3 1 4
样例输出
6
3
数据规模与约定
对于20%的数据n <= 100，m <= 200。
对于50%的数据n <= 5000，m <= 5000。
对于100%的数据1 <= n <= 100000，m <= 100000，0 <= 格⼦权值 <= 10000。
分析：⽤结构体数组建⽴⼀棵线段树~当p==1时从上到下更新这个线段树的值，当p==2的时候搜索对
应区间内的总和~当p==3的时候搜索对应区间的最⼤值

AC：

　　

  #include<iostream>
  using namespace std;
  struct Node{
    int l;
    int r;
    int maxvalue;
    int sum;
  };
  Node a[100000];
  void init(int left, int right, int k){
    a[k].l = left;
    a[k].r = right;
    a[k].maxvalue = 0;
    a[k]. sum = 0;
    if(left != right){
      int mid = (left + right)/2;
      init(left, mid, 2*k);
      init(mid+1, right, 2*k+1);
    }
  }
  void update(int i, int k, int value){
    if(a[i].l == a[i].r){
      a[i].maxvalue = value;
      a[i].sum = value;
      return;
    }
    int mid = (a[i].l + a[i].r)/2;
    if(k <= mid) update(2*i, k, value);
    else update(2*i+1, k, value);
    a[i].maxvalue = max(a[2*i].maxvalue, a[2*i+1].maxvalue);
    a[i].sum = a[2*i].sum + a[2*i+1].sum;
  }
  int query_sum(int i, int x, int y){
    if(x == a[i].l && y == a[i].r) return a[i].sum;
    int mid = (a[i].l + a[i].r)/2;
    if(y <= mid) return query_sum(2*i, x, y);
    else if(x > mid) return query_sum(2*i+1, x, y);
    else return query_sum(2*i, x, mid) + query_sum(2*i+1, mid+1, y);
  }
  int query_max(int i, int x, int y) {
      if(x == a[i].l && y == a[i].r) {
          return a[i].maxvalue;
      }
      int mid = (a[i].l + a[i].r) / 2;
      if(y <= mid)
          return query_max(2*i, x, y);
      else if(x > mid)
          return query_max(2*i+1, x, y);
      else
          return max(query_max(2*i, x, mid), query_max(2*i+1, mid+1, y));
  }
  int main(){
    int n, m;
    cin >> n >> m;
    init(1, n, 1);
    for(int i = 1; i <= n; i++){
      int value;
      cin >> value;
      update(1, i, value);
    }
    for(int i = 0; i < m; i++){
      int op, x, y;
      cin >> op >> x >> y;
      if(op == 1) update(1, x, y);
      if(op == 2) cout << query_max(1, x, y) << endl;
      if(op == 3) cout << query_sum(1, x, y) << endl;
    }
    return 0;
  }