贪心算法的基本要素
1.贪心选择性质
所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。在动态规划算法中,每步所作的选择往往依赖于相关子问题的解。因而只有在解出相关子问题后,才能作出选择。而在贪心算法中,仅在当前状态下作出最好选择,即局部最优选择。然后再去解作出这个选择后产生的相应的子问题。贪心算法所作的贪心选择可以依赖于以往所作过的选择,但决不依赖于将来所作的选择,也不依赖于子问题的解。正是由于这种差别,动态规划算法通常以自底向上的方式解各子问题,而贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为一个规模更小的子问题。
对于一个具体问题,要确定它是否具有贪心选择性质,我们必须证明每一步所作的贪心选择最终导致问题的一个整体最优解。通常可以用我们在证明活动安排问题的贪心选择性质时所采用的方法来证明。首先考察问题的一个整体最优解,并证明可修改这个最优解,使其以贪心选择开始。而且作了贪心选择后,原问题简化为一个规模更小的类似子问题。然后,用数学归纳法证明,通过每一步作贪心选择,最终可得到问题的一个整体最优解。其中,证明贪心选择后的问题简化为规模更小的类似子问题的关键在于利用该问题的最优子结构性质。
2.最优子结构性质
当一个问题的最优解包含着它的子问题的最优解时,称此问题具有最优子结构性质。问题所具有的这个性质是该问题可用动态规划算法或贪心算法求解的一个关键特征。在活动安排问题中,其最优子结构性质表现为:若a是对于正的活动安排问题包含活动1的一个最优解,则相容活动集合a’=a—{1}是对于e’={i∈e:si≥f1}的活动安排问题的一个最优解。
以每个岛的坐标为圆心画圆,会与x轴有2个交点,那么这2个点就是能覆盖该岛的雷达x坐标区间,问题就转变成对一组区间,找最少数目的点,使得所有区间中都有一点。把包含某区间的区间删掉(如果一个点使得子区间得到满足, 那么该区间也将得到满足),这样所有区间的终止位置严格递增。
每次迭代对于第一个区间, 选择最右边一个点, 因为它可以让较多区间得到满足, 如果不选择第一个区间最右一个点(选择前面的点), 那么把它换成最右的点之后, 以前得到满足的区间, 现在仍然得到满足, 所以第一个区间的最右一个点为贪婪选择, 选择该点之后, 将得到满足的区间删掉, 进行下一步迭代, 直到结束。
更一般的形式为差分约束系统
--LRJ
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
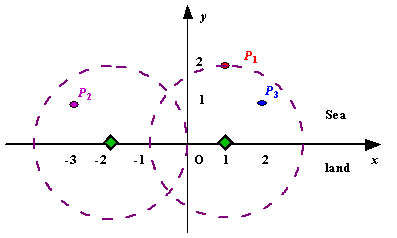
Figure A Sample Input of Radar Installations
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
Sample Output
Case 1: 2
Case 2: 1
Source
Beijing 2002
//
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
struct Range
{
Range(double l, double r):left(l),right(r){};
double left;
double right;
};
class CompareRange
{
public:
bool operator()(const Range& r1, const Range& r2)
{
return r1.left < r2.left;
}
};
int main()
{
vector<Range> rgs;
int n,d;
for(int cases = 1;cin >> n >> d && n; ++cases)
{
rgs.clear();
bool flag = false;
double x, y, temp;
for(int i = 0;i < n; ++i)
{
cin >> x >> y;
if(abs(y) > d) flag = true;
else
{
temp = sqrt(d * d - y * y );
Range range(x - temp, x + temp);
rgs.push_back(range);
}
}
if(flag)
{
cout<<"Case "<<cases<<": -1"<<endl; continue;
}
std::sort(rgs.begin(),rgs.end(),CompareRange());
int ans = 1;
double pre = rgs[0].right;
for(int i = 1; i < n; ++i) {
if(rgs[i].left-pre > 10e-7)
{
++ans;
pre = rgs[i].right;
}
else
{
if(rgs[i].right - pre < 10e-7) pre = rgs[i].right;
}
} cout<<"Case "<<cases<<": "<<ans<<endl;
}
return 0;
}