
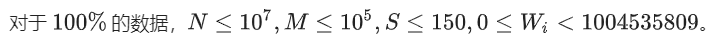
1004535809也是NTT模数,原根为3
(k=min(m,n/s))最多选的颜色数
(g_i,i)个颜色数为s的方案数
[g_i=C_m^iC_n^{si}frac{(si)!}{(s!)^i}(m-i)^{n-si}=C_m^ifrac{n!}{(s!)^i(n-si)!}(m-i)^{n-si}
]
然鹅是错的,实际我们计算的是至少为i的方案数,如果要算恰好为i得用容斥(二项式反演)
[f_i=sum_{j=i}^k(-1)^{j-i}C_j^ig_i
]
拆组合数
[f_i*i!=sum_{j=i}^k(g_j*j!)*(frac{(-1)^{j-i}}{j-i})
]
减法卷积即可
时间复杂度(O(n+mlog))
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read(){
int x=0,f=1;char c=getchar();
while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return f==1?x:-x;
}
const int N=1e7+4,M=1e5+4,mod=1004535809;
inline int ksm(int x,int r){
int ret=1;
for(int i=0;(1ll<<i)<=r;i++){
if((r>>i)&1)(ret*=x)%=mod;
(x*=x)%=mod;
}
return ret;
}
int rev[M<<2];
inline void NTT(int *a,int len,int lim,int fl){
for(int i=0;i<len;i++){
rev[i]=(rev[i>>1]>>1)|((i&1)<<lim-1);
if(i<rev[i])swap(a[i],a[rev[i]]);
}
for(int mid=1,tmp,x,u,v;mid<len;mid<<=1){
tmp=ksm(3,(mod-1)/(mid<<1));
if(fl==-1)tmp=ksm(tmp,mod-2);
for(int i=0;i<len;i+=(mid<<1)){
x=1;
for(int j=0;j<mid;j++,(x*=tmp)%=mod){
u=a[i+j];v=x*a[i+j+mid]%mod;
a[i+j]=(u+v)%mod;a[i+j+mid]=(u-v+mod)%mod;
}
}
}
if(fl==-1)for(int i=0,tmp=ksm(len,mod-2);i<len;i++)
(a[i]*=tmp)%=mod;
}
int n,m,s,k,ans,g[M<<2],a[M<<2],fac[N],inv[N];
signed main(){
fac[0]=fac[1]=inv[0]=inv[1]=1;
for(int i=2;i<=N-4;i++)fac[i]=fac[i-1]*i%mod;
inv[N-4]=ksm(fac[N-4],mod-2);
for(int i=N-5;i>1;i--)inv[i]=inv[i+1]*(i+1)%mod;
n=read();m=read();s=read();
k=min(m,n/s);
for(int i=0,sinv=1;i<=k;i++,(sinv*=inv[s])%=mod){
g[i]=fac[m]*inv[i]%mod*inv[m-i]%mod*fac[n]%mod*sinv%mod*inv[n-s*i]%mod*ksm(m-i,n-s*i)%mod*fac[i]%mod;
a[k-i]=inv[i]*((i&1)?mod-1:1)%mod;
}
int len=1,lim=0;
while(len<=(k<<1)){len<<=1;lim++;}
NTT(g,len,lim,1);NTT(a,len,lim,1);
for(int i=0;i<len;i++)(a[i]*=g[i])%=mod;
NTT(a,len,lim,-1);
for(int i=0;i<=k;i++)
(ans+=a[k+i]*read()%mod*inv[i])%=mod;
cout<<ans;
return (0-0);
}