! FJOI2018领导集团问题

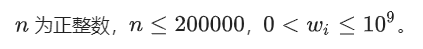
$n^2DP$40pts

选的点不一定连通诶

按w排序，在这个点之前的只要在子树内都可以选，dp+树状数组（错误错误，子树内不满足w）

瞄了眼原题，线段树合并！！？？

究竟何时用线段树合并呢？

w离散化后做下标，不过好麻烦

SOL：

这个问题相当于求树上的LIS

回顾一下序列上，维护一个大到小的单调栈，若当前数是最小的就新建节点，否则找到刚好小于自己的位置，替换那个数

树上用multiset维护单调栈，合并用启发式合并 (ans=s[1].size())

时间复杂度(O(nlog^2))

#include<bits/stdc++.h>
using namespace std;
inline int read(){
	int x=0,f=1;char c=getchar();
	while(!isdigit(c)){if(c=='-')f=-1;c=getchar();}
	while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return f==1?x:-x;
}
const int N=2e5+4;
int n,w[N];
vector<int>e[N];
multiset<int,greater<int>>s[N];
void dfs(int x){
	for(auto v:e[x]){
		dfs(v);
		if(s[x].size()<s[v].size())swap(s[x],s[v]);
		for(auto i:s[v])s[x].insert(i);
		s[v].clear();
	}
	auto it=s[x].upper_bound(w[x]);//
	if(it!=s[x].end())s[x].erase(it);
	s[x].insert(w[x]);
}
int main(){
	n=read();
	for(int i=1;i<=n;i++)w[i]=read();
	for(int i=2;i<=n;i++)e[read()].push_back(i);
	dfs(1);
	cout<<s[1].size();
	return (0-0);
}