3033: 太鼓达人
Time Limit: 1 Sec Memory Limit: 128 MBSubmit: 690 Solved: 497
[Submit][Status][Discuss]
Description
七夕祭上,Vani牵着cl的手,在明亮的灯光和欢乐的气氛中愉快地穿行。这时,在前面忽然出现了一台太鼓达人机台,而在机台前坐着的是刚刚被精英队伍成员XLk、Poet_shy和lydrainbowcat拯救出来的的applepi。看到两人对太鼓达人产生了兴趣,applepi果断闪人,于是cl拿起鼓棒准备挑战。然而即使是在普通难度下,cl的路人本性也充分地暴露了出来。一曲终了,不但没有过关,就连鼓都不灵了。Vani十分过意不去,决定帮助工作人员修鼓。
鼓的主要元件是M个围成一圈的传感器。每个传感器都有开和关两种工作状态,分别用1和0表示。显然,从不同的位置出发沿顺时针方向连续检查K个传感器可以得到M个长度为K的01串。Vani知道这M个01串应该是互不相同的。而且鼓的设计很精密,M会取到可能的最大值。现在Vani已经了解到了K的值,他希望你求出M的值,并给出字典序最小的传感器排布方案。
Input
一个整数K。
Output
一个整数M和一个二进制串,由一个空格分隔。表示可能的最大的M,以及字典序最小的排布方案,字符0表示关,1表示开。你输出的串的第一个字和最后一个字是相邻的。
Sample Input
Sample Output
HINT
得到的8个01串分别是000、001、010、101、011、111、110和100。注意前后是相邻的。长度为3的二进制串总共只有8种,所以M = 8一定是可能的最大值。
对于全部测试点,2≤K≤11。
Source
HOME Back
题解
参照Clove_unique的题解
这道题实际上是将k-1位的二进制数看做点,k位的二进制数看成边,并且连接两个点的边就是将这两个点的权像这样联系起来
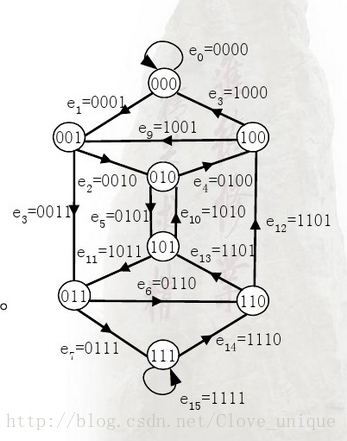
然后每个点的入度和出度相等并且全部是偶点,是一个标准的欧拉图,所以只需要在这个图中找字典序最小的欧拉回路就行了
可以贪心地找字典序较小的边,然后实在不行了就回溯
这样的话时间复杂度是接近O(n+m)的
#include<bits/stdc++.h>
#define rg register
#define il inline
#define co const
template<class T>il T read(){
rg T data=0,w=1;rg char ch=getchar();
for(;!isdigit(ch);ch=getchar())if(ch=='-') w=-w;
for(;isdigit(ch);ch=getchar()) data=data*10+ch-'0';
return data*w;
}
template<class T>il T read(rg T&x) {return x=read<T>();}
typedef long long ll;
co int N=2048;
int p[20],n,t;
bool v[N],ans[N];
bool dfs(int x,int k){
if(v[x]) return 0;
if(k==t) return 1;
ans[k]=x&1;
v[x]=1;
if(dfs((x<<1)&(t-1),k+1)) return 1;
if(dfs((x<<1|1)&(t-1),k+1)) return 1;
v[x]=0;
return 0;
}
int main(){
p[0]=1;
for(int i=1;i<20;++i) p[i]=p[i-1]<<1;
read(n);
printf("%d ",t=p[n]);
dfs(0,1);
for(int i=1;i<n;++i) putchar('0');
for(int i=1;i<=t-n+1;++i) printf("%d",ans[i]);
puts("");
return 0;
}