「NOI2017」泳池

「NOI2017」泳池

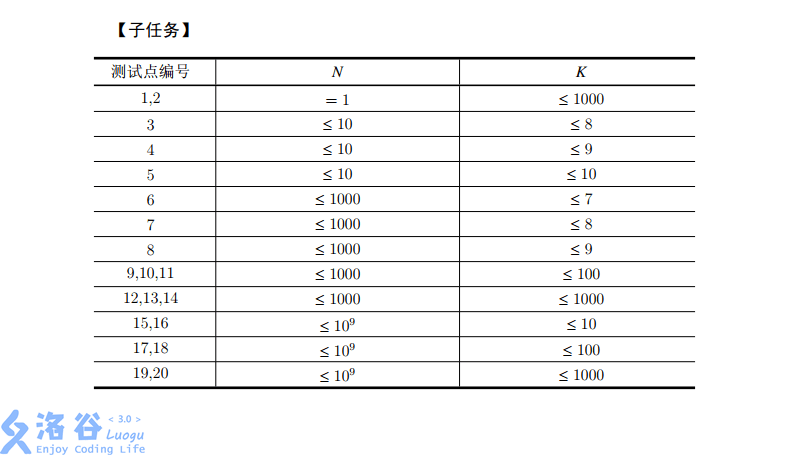
题目背景

久莲是个爱玩的女孩子。

暑假终于到了，久莲决定请她的朋友们来游泳，她打算先在她家的私人海滩外圈一块长方形的海域作为游泳场。然而大海里有着各种各样的危险，有些地方水太深，有些地方有带毒的水母出没。她想让圈出来的这一块海域都是安全的。

题目描述

经过初步的分析，她把这块海域抽象成了一个底边长为$N$米，高为$1001$米的长方形网格。其中网格的底边对应着她家的私人海滩，每一个$1 imes 1$的小正方形都代表着一个单位海域。她拜托了她爸爸明天去测量每一个小正方形是否安全。在得知了信息之后，她要做的就是圈出她想要的游泳场啦。

她心目中理想的游泳场满足如下三个条件：

• 必须保证安全性。即游泳场中的每一个单位海域都是安全的。

• 必须是矩形。即游泳场必须是整个网格中的一个$a imes b$的子网格。

• 必须和海滩相邻。即游泳场的下边界必须紧贴网格的下边界。

例如：当$N = 5$时，若测量的结果如下（因为$1001$太大，这儿只画出网格最下面

三行的信息，其他部分都是危险的）。

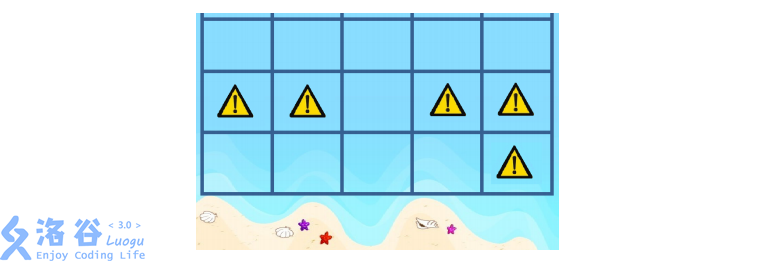
那么她可以选取最下面一行的$1 imes 4$的子海域，也可以选择第三列的$3 imes 1$的子海域。注意她不能选取最上面一行的$1 imes 5$的子海域，因为它没有与海滩相邻。

为了让朋友们玩的开心，她想让游泳场的面积尽可能的大。因此她会选取最下面那一行的$1 imes 4$的子海域作为最终方案。

虽然她要明天才能知道每一个单位海域是否安全，但是她现在就想行动起来估计一下她的游泳场面积有多大。经过简单的估计，她假设每一个单位海域都有独立的$q$的概率是安全的，$1 - q$ 的概率是不安全的。她想要知道她能选择的最大的游泳场的面积恰好为$K$的概率是多少。

然而久莲对数学并不感兴趣，因此她想让你来帮她计算一下这个数值。

输入输出格式

输入格式：

输入一行四个正整数$N, K, x, y$，其中$ 1 leqslant x < y < 998244353$。$q$的取值为$frac{x}{y}$。

输出格式：

输出一行一个整数表示答案在模 $998244353$ 意义下的取值。

即设答案化为最简分式后的形式为 $frac{a}{b}$，其中$a$和$b$的互质。输出整数$x$使得 $ bx equiv a mod {998244353}$ 且 $0 leqslant x < 998244353$。可以证明这样的整数$x$是唯一的。

输入输出样例

输入样例#1： 复制

10 5 1 2

输出样例#1： 复制

342025319

说明

shadowice1984的题解

首先发现求恰好为k不太好做，变成极大子矩形小于k的概率减小于k-1的概率

然后我们设(f_{i})表示这种图形出现的概率：宽为i，底部第i个点恰好是坏点，且这个i×1001的矩形中不存在面积大于等于k的好的极大子矩形。然后我们发现我们的答案就是(frac{f_{n+1}}{1-q})。

那么我们仔细看一下这个(f)数组是可以递推的，我们枚举底部上一个坏点的位置，显然这两个坏点距离不会大于k，不然就会出现一个面积大于等于k的好的子矩形了

那么(f_{x})应该等于这个东西

[f_{x}=sum_{i=1}^{min(k,x)}f_{x-i}p_{i} ]

边界条件(f_{0}=1)

其中(p_{i})应该表示这种图形出现的概率:宽度为i的矩形，且这个i×1001里面不存在面积大于k的极大子矩形。

似乎(p_{i})没有什么优秀的计算方式好像也不能递推……所以我们考虑把(p_{i})拆成一堆数的和，换句话说我们把(p)DP出来

那么我们可以考虑枚举这个矩形坏点高度的最小值

所以我们设(dp_{i,j})表示这种图形的出现概率:宽为i的矩形，坏点高度最小值为j+1，且这个矩形中不会出现面积大于k的极大子矩形

那么我们认真观察一下会发现(dp)数组是可以递推的！

我们可以从高到低的枚举坏点高度的最小值，然后从左到右枚举第一个坏点的位置进行转移，另外显然宽度为i的矩形坏点高度最小值不得超过(lceil frac ki ceil)，所以i×j大于k的dp值我们无需也不能计算出来

那么转移方程大概长这样

[dp_{i,j}=(1-q)q^{j}sum_{t=1}^{i}(sum_{p=j+1}^{infty}dp_{t-1,p})(sum_{p=j}^{infty}dp_{i-t,p}) ]

如果我们记sdp为这个东西(其实就是后缀和)

[sdp_{i,j}=sum_{p=j}^{infty}dp_{i,p} ]

那么转移方程就是

[dp_{i,j}=(1-q)q^{j}sum_{m+n=i-1}sdp_{m,j+1}sdp_{n,j} ]

当然你可以用ntt加上多项式求逆均摊(O(log n))的转移

但是这里暴力卷积就行了因为k只有1000

我们仔细观察一下会发现，如果我们以枚举坏点高度最小值的方式计算p的话我们会发现p大概是这个式子

[p_{i}=sum_{p=1}^{infty}dp_{i,p}=sdp_{i,1} ]

所以我们的p就被求出来了……

那么此时我们的目标是求(f_{n+1})，发现是常系数齐次线性递推的形式，还用不着多项式。

#include<bits/stdc++.h>
#define co const
#define il inline
typedef long long LL;
using namespace std;

co int mod=998244353;
il int add(int a,int b){
	return (a+=b)>=mod?a-mod:a;
}
il int mul(int a,int b){
	return (LL)a*b%mod;
}
int fpow(int a,int b){
	int ans=1;
	for(;b;b>>=1,a=mul(a,a))
		if(b&1) ans=mul(ans,a);
	return ans;
}

co int N=2048;
int n,k,p,q;
int sdp[N][N];
int trans[N],start[N];
int f[N],res[N],a[N],cp[N];
int solve(int k){
	for(int i=0;i<=k+1;++i) sdp[0][i]=1;
	for(int j=k;j>=1;--j)for(int i=1;i*j<=k;++i){
		int&res=sdp[i][j];
		for(int t=1;t<=i;++t) res=add(res,mul(sdp[t-1][j+1],sdp[i-t][j]));
		res=mul(res,mul(p,fpow(q,j)));
		res=add(res,sdp[i][j+1]);
	}
	++k;
	trans[1]=p; //转移系数（含分段坏点概率 ） 
	for(int i=1;i<=k-1;++i) trans[i+1]=mul(sdp[i][1],p);
	start[0]=1; //初值
	for(int i=1;i<k;++i)for(int j=0;j<i;++j)
		start[i]=add(start[i],mul(start[j],trans[i-j]));
	for(int i=1;i<=k;++i) f[k-i]=mod-trans[i];
	f[k]=1;
	res[0]=1,a[1]=1;
	for(int t=n+1;t;t>>=1){
		if(t&1){
			for(int i=0;i<=k;++i) cp[i]=res[i],res[i]=0;
			for(int i=0;i<=k;++i)for(int j=0;j<=k;++j) //卷积
				res[i+j]=add(res[i+j],mul(cp[i],a[j]));
			for(int i=2*k;i>=k;--i)for(int j=0;j<=k;++j) //长除法取模
				res[i-k+j]=add(res[i-k+j],mod-mul(res[i],f[j])); // f[k]=1
		}
		for(int i=0;i<=k;++i) cp[i]=a[i],a[i]=0;
		for(int i=0;i<=k;++i)for(int j=0;j<=k;++j)
			a[i+j]=add(a[i+j],mul(cp[i],cp[j]));
		for(int i=2*k;i>=k;--i)for(int j=0;j<=k;++j)
			a[i-k+j]=add(a[i-k+j],mod-mul(a[i],f[j]));
	}
	int ans=0;
	for(int i=0;i<k;++i) ans=add(ans,mul(start[i],res[i]));
	for(int i=0;i<=k+1;++i) fill(sdp[i],sdp[i]+k+2,0);
	for(int i=0;i<=k;++i) a[i]=res[i]=start[i]=0;
	return mul(ans,fpow(p,mod-2));
}
int main(){
	int x,y;
	scanf("%d%d%d%d",&n,&k,&x,&y);
	q=mul(x,fpow(y,mod-2)),p=add(1,mod-q);
	printf("%d
",add(solve(k),mod-solve(k-1)));
}