填数游戏
小 D 特别喜欢玩游戏。这一天,他在玩一款填数游戏。
这个填数游戏的棋盘是一个 (n imes m) 的矩形表格。玩家需要在表格的每个格子中填入一个数字(数字 (0) 或者数字 (1)),填数时需要满足一些限制。下面我们来具体描述这些限制。
为了方便描述,我们先给出一些定义:
-
我们用每个格子的行列坐标来表示一个格子,即 ((x,y)),其中,(x) 为行坐标,(y) 为列坐标。(注意:行列坐标均从 (0) 开始编号);
-
合法路径 (P):一条路径是合法的当且仅当:
-
这条路径从矩形表格的左上角的格子 ((0,0)) 出发,到矩形的右下角格子 ((n-1,m-1)) 结束;
-
在这条路径中,每次只能从当前的格子移动到右边与它相邻的格子,或者从当前格子移动到下面与它相邻的格子。
-
例如:在下面这个矩形中,只有两条路径是合法的,它们分别是 (P_1:(0,0) o (0,1) o (1,1), P_2:(0,0) o (1,0) o (1,1))。
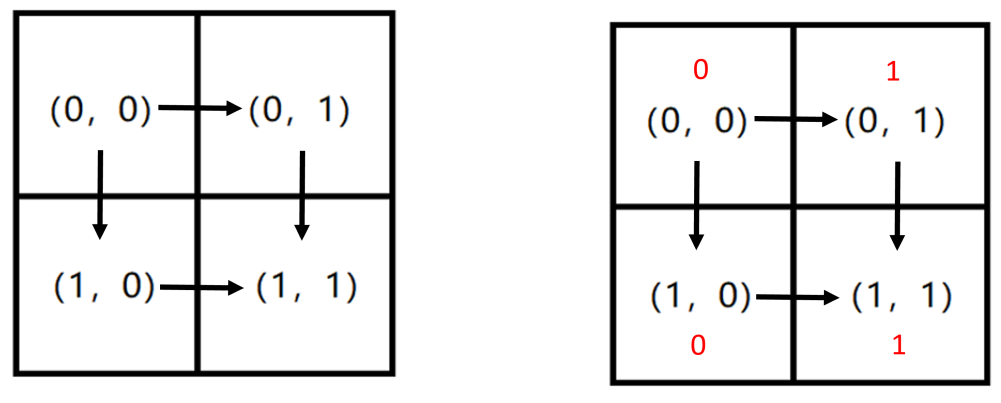
对于一条合法的路径 (P),我们可以用一个字符串 (w(P)) 来表示,该字符串的长度为 (n+m-2),其中只包含字符 R 或者字符 D,第 (i) 个字符记录了路径 (P) 中第 (i) 步的移动方法,R 表示移动到当前格子右边与它相邻的格子,D 表示移动到当前格子下面与它相邻的格子。例如,上图中对于路径 (P_1),有 (w(P_1)= exttt{RD});而对于另一条路径 (P_2),有 (w(P_2)= exttt{DR})。
同时,将每条合法路径 (P) 经过的每个格子上填入的数字依次连接后,会得到一个长度为 (n+m-1) 的 (01) 字符串,记为 (s(P))。例如,如果我们在格子 ((0,0)) 和 ((1,0)) 上填入数字 (0),在格子 ((0,1)) 和 ((1,1)) 上填入数字 (1)(见上图红色数字)。那么对于路径 (P_1),我们可以得到 (s(P_1)= exttt{011}),对于路径 (P_2),有 (s(P_2)= exttt{001})。
游戏要求小 D 找到一种填数字 (0,1) 的方法,使得对于两条路径 (P_1,P_2),如果 (w(P_1)gt w(P_2)),那么必须 (s(P_1)le s(P_2))。我们说字符串 (a) 比字符串 (b) 小,当且仅当字符串 (a) 的字典序小于字符串 (b) 的字典序,字典序的定义详见第 1 题。但是仅仅是找 (1) 种方法无法满足小 D 的好奇心,小 D 更想知道这个游戏有多少种玩法,也就是说,有多少种填数字的方法满组游戏的要求?
小 D 能力有限,希望你帮助他解决这个问题,即有多少种填 (0,1) 的方法能满足题目要求。由于答案可能很大,你需要输出答案对 (10^9+7) 取模的结果。
题解
耳濡目染地做了这道题:DFS打表,发现等比数列。
性质:
-
对于每一个斜行,其 (0/1) 状态一定是存在一个分界点,使得其左下方都是 (1),其右上方都是 (0)。
-
(ans(n,m)=ans(m,n)),反转一下 (0/1) 就能发现。
-
如果某一个格子它左边上边的两个格子的 (0/1) 是相同的,或者它左边或上边有格子是模糊点,那这个格子就是模糊点;模糊点右边下边的两个格子的 (0/1) 必须相同。
满足这几条性质的矩阵一定是合法的,所以就可以打表了。(n=m=8) 的数据都能在 1s 中跑出来。
| nm | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | |
| 2 | 4 | 12 | 36 | 108 | 324 | 972 | 2916 | 8748 | |
| 3 | 8 | 36 | 112 | 336 | 1008 | 3024 | 9072 | 27216 | |
| 4 | 16 | 108 | 336 | 912 | 2688 | 8064 | 2419 | 272576 | |
| 5 | 32 | 324 | 1008 | 2688 | 7136 | 21312 | 63936 | 191808 | |
| 6 | 64 | 972 | 3024 | 8064 | 21312 | 56768 | 170112 | 510336 | 1531008 |
| 7 | 128 | 2916 | 9072 | 24192 | 63936 | 170112 | 453504 | 1360128 | 4080384 |
| 8 | 256 | 8748 | 27216 | 272576 | 191808 | 510336 | 1360128 | 3626752 | 10879488 |
发现当 (m≥n+1) 时答案是等比数列,所以打个表即可。
打表程序:
int n,m;
struct crd {int x,y;}; // coordinate
vector<crd> col[100]; // column
int wei[100][100],vis[100][100];
int ans;
IN void dye(CO crd&p,int w){
wei[p.x][p.y]=w;
}
IN void visit(CO crd&p){
vis[p.x][p.y+1]=1;
}
void dfs(int x){
if(x==n+m){
// puts("matrix=");
// for(int i=1;i<=n;++i)
// for(int j=1;j<=m;++j) printf("%d%c",wei[i][j],"
"[j==m]);
// puts("vis=");
// for(int i=1;i<=n;++i)
// for(int j=1;j<=m;++j) printf("%d%c",vis[i][j],"
"[j==m]);
++ans;
return;
}
for(int i=0;i<(int)col[x].size();++i){
CO crd&p=col[x][i];
if(p.x>1 and vis[p.x-1][p.y]) vis[p.x][p.y]=1;
if(p.y>1 and vis[p.x][p.y-1]) vis[p.x][p.y]=1;
}
for(int i=0;i<=(int)col[x].size();++i){
if(i>0 and i<(int)col[x].size()){
CO crd&p=col[x][i];
if(vis[p.x][p.y-1]) continue;
}
if(x<n+m-1){
for(int i=0;i<(int)col[x+1].size();++i){
CO crd&p=col[x+1][i];
vis[p.x][p.y]=0;
}
}
for(int j=0;j+1<=i;++j) dye(col[x][j],1);
for(int j=0;j+1<=i-1;++j) visit(col[x][j]);
for(int j=i;j<(int)col[x].size();++j) dye(col[x][j],0);
for(int j=i;j<(int)col[x].size()-1;++j) visit(col[x][j]);
dfs(x+1);
}
}
int main(){
// freopen("game.out","w",stdout);
read(n),read(m);
if(n>m) swap(n,m);
for(int i=1;i<=n;++i){
col[i].push_back((crd){i,1});
while(col[i].back().x>1)
col[i].push_back((crd){col[i].back().x-1,col[i].back().y+1});
}
for(int i=n+1;i<=m-1;++i){
col[i].push_back((crd){n,i-n+1});
while(col[i].back().x>1)
col[i].push_back((crd){col[i].back().x-1,col[i].back().y+1});
}
for(int i=max(n+1,m);i<=n+m-1;++i){
col[i].push_back((crd){n,i-n+1});
while(col[i].back().y<m)
col[i].push_back((crd){col[i].back().x-1,col[i].back().y+1});
}
dfs(1);
printf("%d
",ans);
return 0;
}
AC程序:
int main(){
freopen("game.in","r",stdin),freopen("game.out","w",stdout);
int n=read<int>(),m=read<int>();
if(n>m) swap(n,m);
switch(n){
case 1:{
printf("%d
",fpow(2,m));
break;
}
case 2:{
if(m==2) puts("12");
else printf("%d
",mul(36,fpow(3,m-3)));
break;
}
case 3:{
if(m==3) puts("112");
else printf("%d
",mul(336,fpow(3,m-4)));
break;
}
case 4:{
if(m==4) puts("912");
else printf("%d
",mul(2688,fpow(3,m-5)));
break;
}
case 5:{
if(m==5) puts("7136");
else printf("%d
",mul(21312,fpow(3,m-6)));
break;
}
case 6:{
if(m==6) puts("56768");
else printf("%d
",mul(170112,fpow(3,m-7)));
break;
}
case 7:{
if(m==7) puts("453504");
else printf("%d
",mul(1360128,fpow(3,m-8)));
break;
}
case 8:{
if(m==8) puts("3626752");
else printf("%d
",mul(10879488,fpow(3,m-9)));
break;
}
}
return 0;
}