LOJ2882 两个人的星座

两个人的星座

JOI 酱和 IOI 酱是一对亲密无间的好朋友。某天，JOI 酱与 IOI 酱决定去山上的某个观象台进行天体观测。

从观象台上可以观测到 (N) 颗星星，编号为 (1dots N)。每颗星星的颜色为红色、蓝色、黄色中的一种。

在观象台上观测到的星星可以用坐标系上的点来表示。在坐标系上，(i) 号星对应的点为 (P_i)，位于 ((X_i,Y_i))。坐标系上的点两两不同，且不存在三点共线。

JOI 酱和 IOI 酱想要设立一个叫做「JOIOI 座」的星座。首先。两个人决定使用红色、蓝色、黄色三种颜色的星各一个构成的三角形。他们将这样的三角形称作「好三角形」。

两人将满足以下条件的一对（两个，无序）好三角形作为「JOIOI 座的候补」：

• 两个三角形没有公共点（包括内部和边界）。换言之，两个三角形之间既不相交，也不存在某个三角形包含另一个三角形。

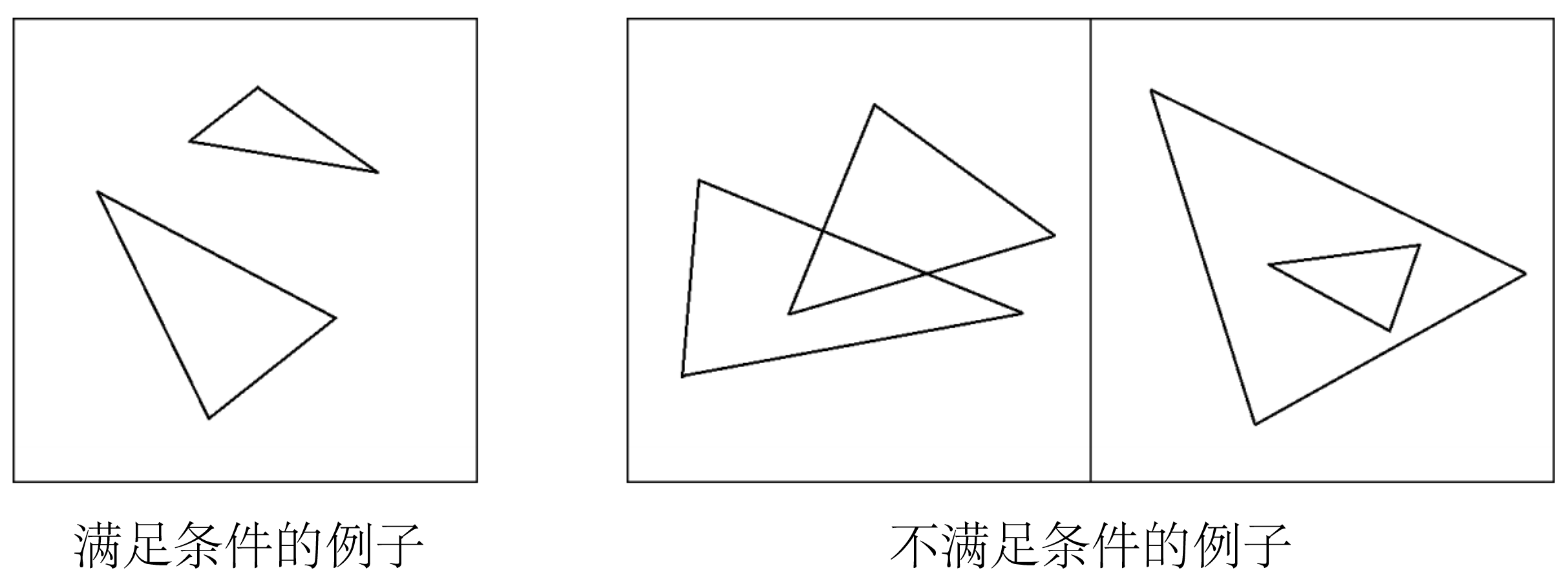
JOI 酱和 IOI 酱想知道构成 JOIOI 座的候补一共有多少种方案。

注意，如果构成三角形的 (6) 个点一样，但是构成三角形的方式不同，算作不同的方案。

现在给出观象台上能观测到的星星的信息，请求出构成「JOIOI 座的候补」一共有多少种方案。

对于所有数据，(6le Nle 3000,) (-10^5le X_i, Y_ile 10^5,) (C_i=0) 或 (1) 或 (2)，保证任何一种颜色的星星都有至少一颗，星星坐标互不相同，无三星共线。

题解

http://jklover.hs-blog.cf/2020/04/13/Loj-2882-两个人的星座/#more

两个三角形如果相离，则一定可以用公切线分开。

枚举两个点的连线作为公切线，统计两个半平面中各类颜色点的数目，时间复杂度(O(n^3))。

优化一下，先枚举一个点作为原点，对其他点极角排序。

再枚举另一个点，用前缀和询问两个半平面中各类颜色点的数目。

由于两个相离的三角形通过顶点相连可以产生4根公切线，其中有2根对使得这对三角形被统计到，所以最后还需要将答案除以2。

时间复杂度(O(n^2log n))。

IN int sign(int64 x){
	return x>=0;
}

struct point {int64 x,y;int c;};

IN point operator-(CO point&a,CO point&b){
	return {a.x-b.x,a.y-b.y,a.c};
}
IN int64 cross(CO point&a,CO point&b){
	return a.x*b.y-a.y*b.x;
}
IN bool operator<(CO point&a,CO point&b){
	return sign(a.y)!=sign(b.y)?sign(a.y)>sign(b.y):cross(a,b)>0;
}

CO int N=3e3+10;
int n;
point p[N],q[N];
int sum[N][3],tmp[2][3];

int query(int l,int r,int c){
	if(l>r) return 0;
	return sum[r][c]-sum[l-1][c];
}
int64 solve(){
	for(int i=2;i<=n;++i) q[i-1]=p[i]-p[1];
	sort(q+1,q+n);
	for(int i=1;i<n;++i)
		copy(sum[i-1],sum[i-1]+3,sum[i]),++sum[i][q[i].c];
	int64 ans=0;
	for(int i=1;i<n;++i){
		point iq=(point){0,0}-q[i];
		int l=i,r=lower_bound(q+1,q+n,iq)-q;
		for(int j=0;j<3;++j){
			tmp[0][j]=query(1,l-1,j)+query(r,n-1,j);
			tmp[1][j]=query(l+1,r-1,j);
		}
		int c=p[1].c,d=q[i].c;
		for(int cur=0;cur<2;++cur){
			int64 prod=1;
			for(int j=0;j<3;++j){
				if(c!=j) prod*=tmp[cur][j];
				if(d!=j) prod*=tmp[cur^1][j];
			}
			ans+=prod;
		}
	}
	return ans;
}
int main(){
	read(n);
	for(int i=1;i<=n;++i) read(p[i].x),read(p[i].y),read(p[i].c);
	int64 ans=0;
	for(int i=1;i<=n;++i){
		swap(p[1],p[i]);
		ans+=solve();
		swap(p[1],p[i]);
	}
	printf("%lld
",ans/=2);
	return 0;
}