test20190901 NOI2019 模拟赛

0+0+0=0。还是太菜，看不出题型。

Masodik

你要从 (0,0) 点走到 (n,m)，每次只能往 x 轴或者 y 轴正方向移动一个单位距离。从 (i,j) 移动到 (i,j+1) 的代价为 r_i,从 (i,j) 移动到 (i+1,j) 的代价为 c_j。

求最小代价。

对于 100%的数据，n,m ≤ 10⁵。

题解

凸包的运用……我看不出来还算正常。

考虑从 ((x_1,y_1)) 走到 ((x_2,y_2))，只能先走行再走列或者先走列再走行。

1. 先走行再走列，代价为

   [r_{x_1}(y_2-y_1)+c_{y_2}(x_2-x_1) ]

2. 先走列再走行，代价为

   [c_{y_1}(x_2-x_1)+r_{x_2}(y_2-y_1) ]

对这两种走法进行套路化比较

[r_{x_1}(y_2-y_1)+c_{y_2}(x_2-x_1)<c_{y_1}(x_2-x_1)+r_{x_2}(y_2-y_1)\ Rightarrow~frac{r_{x_2}-r_{x_1}}{x_2-x_1}>frac{c_{y_2}-c_{y_1}}{y_2-y_1} ]

所以对行列分别维护凸包，双指针扫描，每次走斜率大的。

时间复杂度 (O(n+m))。

#include<bits/stdc++.h>
using namespace std;
template<class T> T read(){
	T x=0,w=1;char c=getchar();
	for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*w;
}
template<class T> T read(T&x){
	return x=read<T>();
}
#define co const
#define il inline
typedef long long LL;

co int N=100000+10;
int r[N],c[N];
int sr[N],tr,sc[N],tc;

void convex(int a[],int st[],int&top,int n){
	for(int i=0;i<=n;++i){
		while(top>=2&& (LL)(a[i]-a[st[top]])*(st[top]-st[top-1])<=(LL)(a[st[top]]-a[st[top-1]])*(i-st[top]) ) --top;
		st[++top]=i;
	}
}
int main(){
	freopen("masodik.in","r",stdin),freopen("masodik.out","w",stdout);
	int n=read<int>(),m=read<int>();
	for(int i=0;i<=n;++i) read(r[i]);
	for(int i=0;i<=m;++i) read(c[i]);
	convex(r,sr,tr,n),convex(c,sc,tc,m);
	LL ans=0;
	int i=1,j=1;
	while(i<tr&&j<tc){
		if( (LL)(r[sr[i+1]]-r[sr[i]])*(sc[j+1]-sc[j])>=(LL)(c[sc[j+1]]-c[sc[j]])*(sr[i+1]-sr[i]) )
			ans+=(LL)r[sr[i]]*(sc[j+1]-sc[j]),++j;
		else ans+=(LL)c[sc[j]]*(sr[i+1]-sr[i]),++i;
	}
	if(i==tr) ans+=(LL)r[n]*(m-sc[j]);
	else ans+=(LL)c[m]*(n-sr[i]);
	printf("%lld
",ans);
	return 0;
}

Query on a sequence

给定一个长度为 n 的数列 P，满足 |Pi| ≤ 10⁹
求有多少对 (a,b,c,d)，满足下列约束：

1. 1 ≤ a ≤ b < c ≤ d ≤ n
2. b-a=d-c
3. c-b-1 等于恰好等于给定的 F，且 F>0
4. P_a+i=P_c+i 对于所有 i(0≤i≤b-a) 均成立

只要 (a,b,c,d) 中有任意一个参数不同，我们就认为是不同的。

n ≤ 10⁵

CH#15 秘密武器

被题目名字骗了，我竟然没有看出来这是字符串匹配……我该更新自己对字符集的认识。

枚举两段的长度 len 和第一段的起点 i，我们定义 L 为第一段与第二段的最长公共后缀，当 L>=len 的时候答案+1，而起点为 i+1 时 L 的大小仅仅取决于起点为 i 时 L 大小和 a[i+len] 与 a[i+2*len+F] 的相等关系：

• L[i+1] = L[i] + 1 (a[i+len]=a[i+2*len+F])
• L[i+1] = 0 (a[i+len]!=a[i+2*len+F])

这样相当于把原串右移 len+F 后得到的新串与原串的匹配

朴素地枚举 len 后扫描整个序列是 N² 的，我们考虑优化这个算法。

首先枚举两段的长度 len，然后我们在递推的时候可以发现，在长度为 len 时，我们没有必要一格一格的递推，而可以每次向右递推 len 格。这是因为我们把原串按照 len 分段，出现下面这种红色匹配是无意义的

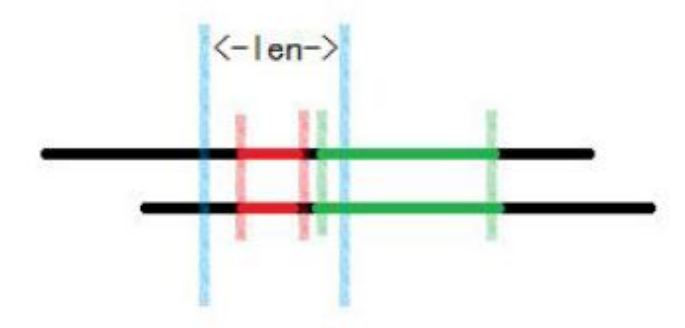
我们不妨设第一段的末尾位置为 i，第二段的末尾位置为 j，设 frontL 表示 a[i+1]„a[i+len] 与 a[j+1]„a[j+len] 的最长公共前缀，设 backL 表示 a[i+1]„a[i+len] 与 a[j+1]„a[j+len] 的最长公共后缀，令 L 表示当前的最长公共后缀。

下面分两种情况考虑对于答案的贡献：

1. 如果 L>=len-1，ans+=frontL。
2. 反之，ans+=max{0,L+frontL-(len-1)}。

下面分两种情况考虑递推后的最长公共后缀 nL:

1. 如果 a[i+1]„a[i+len]与 a[j+1]„a[j+len]整段相同，nL=L+len。
2. 反之，nL=backL。

这样对于每个长度 len，需要递推 N/len 次，每次采用 hash+二分的方法 O(logN) 的计算最长公共前/后缀，总的复杂度为 O(N lnN logN)。

#include<bits/stdc++.h>
#include<tr1/unordered_map>
using namespace std;
template<class T> T read(){
	T x=0,w=1;char c=getchar();
	for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*w;
}
template<class T> T read(T&x){
	return x=read<T>();
}
#define co const
#define il inline
typedef unsigned long long ULL;

co int N=100000+10;
co ULL B=131;
int n,a[N];
ULL hash[N],pb[N];

il ULL calc(int l,int r){ // hash[l,r]
	return hash[r]-hash[l-1]*pb[r-l+1];
}
int lcp(int x,int y){ // longest common prefix
	int l=0,r=min(n-x+1,n-y+1);
	while(l<r){
		int mid=(l+r+1)>>1;
		if(calc(x,x+mid-1)==calc(y,y+mid-1)) l=mid;
		else r=mid-1;
	}
	return l;
}
int lcs(int x,int y){ // longest common suffix
	int l=0,r=min(x,y);
	while(l<r){
		int mid=(l+r+1)>>1;
		if(calc(x-mid+1,x)==calc(y-mid+1,y)) l=mid;
		else r=mid-1;
	}
	return l;
}

int main(){
	freopen("count.in","r",stdin),freopen("count.out","w",stdout);
	read(n);int F=read<int>();
	pb[0]=1;
	for(int i=1;i<=n;++i) pb[i]=pb[i-1]*B;
	tr1::unordered_map<int,int> val;
	int idx=0;
	for(int i=1;i<=n;++i){
		if(!val.count(read(a[i]))) val[a[i]]=++idx;
		a[i]=val[a[i]],hash[i]=hash[i-1]*B+a[i];
	}
	ULL ans=0;
	for(int len=1;2*len+F<=n;++len){
		int L=0;
		for(int i=1;;){
			int lim=min(len,n-(i+len+F-1));
			if(!lim) break;
			int frontL=lcp(i,i+len+F),backL=lcs(i+lim-1,i+len+F+lim-1);
			frontL=min(frontL,lim),backL=min(backL,lim);
			if(L>=len-1) ans+=frontL;
			else ans+=max(0,L+frontL-(len-1));
			if(frontL==lim) L+=lim;
			else L=backL;
			i+=lim;
		}
	}
	printf("%llu
",ans);
	return 0;
}

Number Theory

对于给定的 (x,m,p)（(p) 是质数），求一个可行的正整数 (n)，满足

[n^{2n}+n^{m} equiv x mod p ]

由于解不唯一，所以这题设有 Special Judge，支持检验高精度的 (n)。

(p leq 10^9+7)，可以认为这些质数都很大且随机生成。

题解

原根的运用……我一 NOIP 考生不会往这边想啊。

这是不是一种新的做二次剩余的方法？

#include<bits/stdc++.h>
#include<tr1/unordered_map>
using namespace std;
template<class T> T read(){
	T x=0,w=1;char c=getchar();
	for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
	for(;isdigit(c);c=getchar()) x=x*10+c-'0';
	return x*w;
}
template<class T> T read(T&x){
	return x=read<T>();
}
#define co const
#define il inline
#define int long long

#define gcd __gcd
void exgcd(int a,int b,int&x,int&y){
	if(!b) x=1,y=0;
	else exgcd(b,a%b,y,x),y-=a/b*x;
}
il int inv(int a,int mod){
	int x,y;
	exgcd(a,mod,x,y);
	return x<0?x+mod:x;
}
il int mul(int a,int b,int mod){
	int ans=0;
	for(;b;b>>=1,a=(a+a)%mod)
		if(b&1) ans=(ans+a)%mod;
	return ans;
}
il int pow(int a,int b,int mod){
	int ans=1;
	for(;b;b>>=1,a=a*a%mod)
		if(b&1) ans=ans*a%mod;
	return ans;
}
int bsgs(int a,int b,int mod){
	tr1::unordered_map<int,int> H;
	int blo=ceil(sqrt(mod));
	for(int i=1;i<=blo;++i) H[pow(a,i,mod)*b%mod]=i;
	a=pow(a,blo,mod);
	for(int i=1,c=a;i<=(mod+blo-1)/blo;++i,c=c*a%mod)
		if(H[c]) return i*blo-H[c];
	return -1;
}
signed main(){
	freopen("theory.in","r",stdin),freopen("theory.out","w",stdout);
	int sum=read<int>(),m=read<int>(),p=read<int>();
	for(int g=2;;++g){ // enumerate the primitive root
		int k=bsgs(g,(sum+p-pow(g,m,p))%p,p); // g^k=sum-g^m (mod p)
		if(k==-1||k&1) continue;
		int M=p*(p-1);
		printf("%lld
",mul(g*(p-1),inv(p-1,p),M)+k/2*p%M); // p^{-1}=1 (mod p-1)
		break;
	}
	return 0;
}