动态规划几类例题的笔记

　　蒟蒻乱写一通关于动态规划几类问题的笔记，可能会有错误之处，欢迎指正。

 

一. 01背包问题

　　关于这个问题，我之前已经写了不太全面的（比较扯淡的）笔记，就不复述了。

　　传送门：背包问题学习笔记

　　补充一下除了01背包、完全背包、多重背包外，还有一个超大背包问题值得了解。

二. 最长上升子序列问题（LIS）

　　题目链接：洛谷oj AT2827 LIS　　推荐题解：动态规划——最长上升子序列问题

　　题目不赘述了，LIS就是最长上升子序列。简单来说，就是在一串给定的数列a[n]中取出一些数（未必要连续），让它们能单调上升，并且这个数列要最长。

　　举个例子，对于长度为10的数列“1，9，11，2，10，7，8，9，13，6”，它的LIS就是“1，2，7，8，9，13”，长度为6。

　　对于这个问题，有两种算法，复杂度分别为O(n²)和O(nlogn)。虽然我们发现O(n²)的算法是无法AC洛谷的LIS板子题的，但是O(n²)的算法思想仍然有助于我们理解动态规划。

O(n²)的经典算法：

　　根据动态规划把大问题拆成小问题，分段求解的思路，我们声明一个数组f[maxn]，f[i]表示从1到i中，以a[i]结尾的最长上升子序列的长度。初始时f[i]=1,i∈[1,n]。（初始值其实就是这个序列中只有a[i]时的序列长度，显然为1）。

　　可以写出状态转移方程：f[i]=max{f[j]+1}, j∈[1,i-1]且a[j]<a[i];

　　怎么理解这个方程呢？就是说，当我们已经处理完了f[i-1]，需要求f[i]时，只需要遍历一遍a[1…i-1]，找到所有能成为a[i]前驱的数a[j]（即a[i]>a[j]），然后在所有能成为前驱的a[j]中找到f[j]最大的那个就可以了。如果还不理解，可以尝试直接看代码。

　　因为代码是写出来便于理解的，我就不写寄存器内联快速读入之类花里胡哨的东西了嘻嘻嘻。

#include <cstdio>
using namespace std;
const int maxn=100000;

int n,a[maxn+5],f[maxn+5];
int result;

int main(){
    scanf("%d",&n);
    for (int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        f[i]=1;
    }
    for (int i=1;i<=n;i++)
        for (int j=1;j<i;j++)
            if (a[i]>a[j]&&f[i]<f[j]+1)
                f[i]=f[j]+1;
    for (int i=1;i<=n;i++)
        if (result<f[i])    result=f[i];
    printf("%d",result);
    return 0;
} 

O(nlogn)的优秀算法：

　　如果想优化上面的算法，基于贪心的思想，我们很容易想到：当x,y∈[1,i-1]时，若f[x]=f[y]，a[x]<a[y]，显然f[i]=f[x]+1比f[i]=f[y]+1更优，更可能得到答案。

　　所以在f[x]一定的情况下，尽量选择更小的a[x]。按f[x]=k来分类，我们需要记录的当所有等于k的f[x]中，最小的a[x]。我们声明一个low[k]来存储这个最小的a[x]。

　　这样说可能会有点乱，简单说吧，就是声明一个low[k]，存储在[1,i-1]之间，已知的最长上升子序列长度为k的最小的a[x]值。（还是感觉比较复杂，将就理解一下吧）

　　　　low[k]=min{a[x]},f[x]=k；

　　可以归纳出low[k]的几个性质：

　　　　①low[x]单调递减增，即low[1]＜low[2]＜low[3]＜low[4]＜……＜low[n-1]＜low[n];

　　　　②随着处理时间推进，low[x]只会越来越小;

　　如果不能理解，可以尝试自己写个数列模拟看看。

　　有了这两个性质，就可以这样求解：

　　声明当前已求出的最长上升子序列的长度为len（初始时为1），当读入一个新元素x：

　　　　①若x>low[len]，则直接把x加入到d的末尾，且len+＝1；

　　　　②否则，在low[x]中二分查找，找到第一个比x小的数low[k]，并low[k+1]=x，在这里x<=g[k+1]一定成立。

　　易证时间复杂度为O(nlogn)。

　　代码中的二分查找我用stl的lower_bound函数代替了，但是不开O2会慢挺多吧……手写二分应该会快，蒟蒻我太懒了orz

#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn=100000;

int n,len=1;
int a[maxn+5],low[maxn+5];

int main(){
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    low[1]=a[1];
    for (int i=2,j=0;i<=n;i++){
        if (low[len]<a[i])    j=++len;
        else    j=lower_bound(low+1,low+len+1,a[i])-(low+1)+1;    //这里用stl里的lower_bound代替手写的二分查询 
        low[j]=a[i];
    }
    printf("%d",len);
} 

 三. 最长公共子序列问题（LCS）

　　题目链接：洛谷oj P1439 【模板】最长公共子序列　　推荐题解：《挑战程序设计竞赛（第二版）》2.3

　　注意，这次是最长公共子序列（LCS）。LCS就是指给定两个数列，两个数列中最长的公共子序列（哇我在说什么废话）。

　　举个例子好了，比如下面两个长度分别为6的子序列：

　　　　1 4 9 10 2 6

　　　　2 1 10 2 13 6

　　上面两个子序列，它们的LCS就是长度为4的序列： 1 10 2 6 。和LIS一样，子序列是不需要连续的。

　　为了解决这个问题，我们可以尝试这样思考：

　　首先，记给定的两个序列为s和t，依旧是根据动态规划分段求解的思想。定义f[i][j]为序列 s₁…s_i 和序列 t₁…t_j 对应的LCS的长度。

　　那么f[i+1][j+1]有三种情况：

　　　　① s_i+1=t_i+1时，在序列 s₁…s_i 和序列 t₁…t_j 对应的LCS后面追加s_i+1（s_i+1=t_i+1）；

　　　　② 继承序列 s₁…s_i 和序列 t₁…t_j+1 对应的LCS；

　　　　③ 继承序列 s₁…s_i+1 和序列 t₁…t_j 对应的LCS；

　　f[i][j]为上面三种情况中最大的一个。所以可以写出递推式：

　　　　

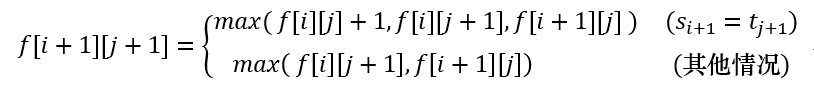
　　这个递推式可以在O(n²)的时间内被计算出来，f[n][n]是LCS的长度。