正规方程
在先学习正规方程之前,先来复习一下之前学过的常规的回归方程的解法。
假设存在如果的代价函数,
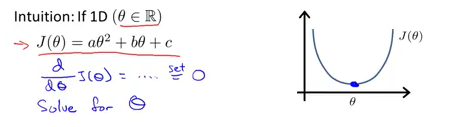
,解法也十分的简答。
但是有时候遇到的情况或许会变得相当的复杂。
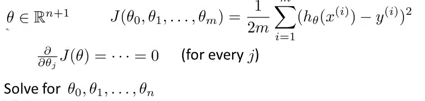
的数,如果是按照常规的方式进行求解,那么按照之前的求解方式,就需要对每一个theta进行微分,然后综合求最小值,这样的运算结果可能最后是相当的复杂。
那么这个时候正规方程就非常有用了。
正规方程对于theat的求解非常的简单,如下:
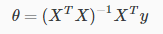
如何求解theta,
还是房价的例子,在房价中,假设房价与房屋面积,房间数量,房间位于的楼层,房间的年限有关,最终得到的训练数据如下:
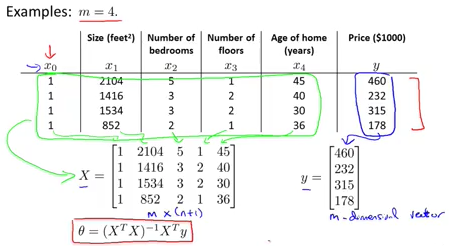
最后求得的theta的结果为:
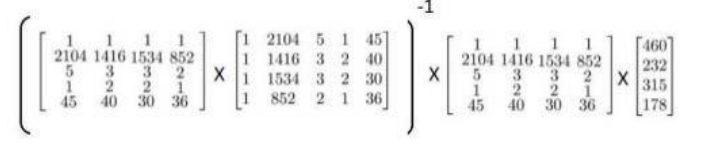
当的简单
正规方程与梯度下降算法的比较
由于使用markdwon不是很好画图,这里就直接使用列表的方式来显示了。
梯度下降算法的优缺点
- 需要选择学习率a
- 需要进行多次迭代
- 当特征(n)非常多时,算法效果很好
- 适用于各种类型的模型
正规方程算法的优缺点
- 不需要学习率
- 不需要进行迭代
- 需要计算转置、逆矩阵等算法
- 不适用于n比较大的情况,当n<10000时,还可以接受
- 仅仅适用于线性模型,不适合逻辑回归等其他的分类模型
总体来说,当特征数量不是很大的时候(小于10000),标准方程是一个很好的计算参数theta的替代方法。
其他
有一点需要注意的时候,在使用正规方程的时候,需要计算
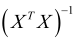
么就是否意味着无法进行下去了?
在Octave中,正规方程的写法是:
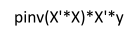
inv()方法还是能够处理。当然这种处理方式其实上还是借助于第三方的计算工具解决问题。
如果在计算机中真的出现了不可逆的举证,有可能是一下两种情况:
- 重复的特征,例如在房价的例子中,存在两个房屋面积的特征x1和x2。x1的单位是英尺,x2的单位是平方米。英尺和米是可以相互转换的,这样就导致这两个特征有一个是重复多余,这样就有可能导致不可逆。处理方法也很简单,直接去掉一个即可。
- 过多的特征,特征的数量n大于样本数量m。例如样本数量只有10个,但是特征数量有100个,这样也有可能会导致不可逆。处理的方式也很简单,删除一些特征或者是使用正规化的线性代数的方法。
为了了能到远方,脚下的每一步都不能少