施密特正交化

对于一组向量，有时候我们需要对其进行正交化处理，也就是说，该组向量中任意两个向量都是互相垂直的。那么，要怎么做呢？

假设只有两个向量，(vec v_0)和(vec v_1)，正交化的几何示意图如下所示。

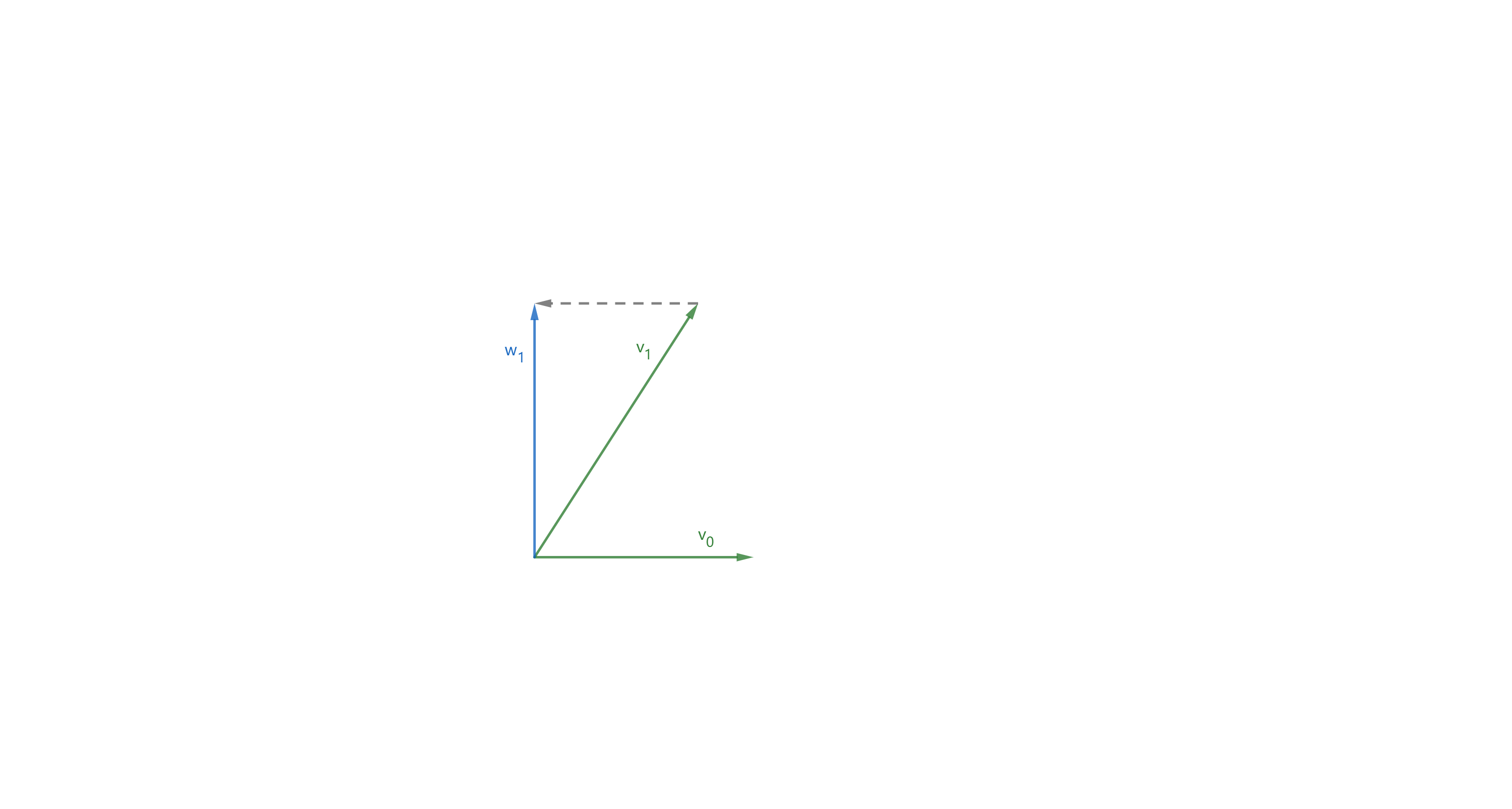
假设正交化之后的向量为(vec w_0)和(vec w_1)，那么由图可知，可得(vec w_0 = vec v_0)，且有：

(vec w_1 = vec v_1 - dfrac{vec v_1 cdot vec w_0}{|vec w_0|})

这里减去的部分是向量(vec v_1)在向量(vec w_0)上的投影。然后将(vec w_0)和(vec w_1)进行归一化，就得到了最终的结果。

那么，如果有三个向量，(vec v_0)，(vec v_1)，(vec v_2)，这种情况要如何处理呢？同样地，正交化的几何示意图如下所示。

假设正交化之后的向量为(vec w_0)，(vec w_1)，(vec w_2)，由图可知，可得(vec w_0 = vec v_0)，且有：

(vec w_1 = vec v_1 - dfrac{vec v_1 cdot vec w_0}{|vec w_0|})

(vec w_2 = vec v_2 - dfrac{vec v_2 cdot vec w_0}{|vec w_0|} - dfrac{vec v_2 cdot vec w_1}{|vec w_1|})

从图中可以看出向量(vec w_2)即为向量(vec v_2)减去在(vec w_0)和(vec w_1)上的投影。将这三个向量进行归一化即可得到最终的结果。

那么，假如我们有一组向量({ vec v_0, vec v_1, vec v_2, ..., vec v_n })，要想求得它们正交化后的向量组({ vec w_0, vec w_1, vec w_2, ..., vec w_n })，步骤如下：

1. 令(vec w_0 = vec v_0)；
2. 计算(vec w_i = vec v_i - sum_{j = 0}^{i - 1} dfrac{vec v_i cdot vec w_j}{|vec w_j |};1 leq i leq n)；
3. 将得到的({ vec w_0, vec w_1, vec w_2, ..., vec w_n })进行正交化。