LeetCode：11.盛最多水的容器

1、题目描述

给定 n 个非负整数 a1，a2，...，an，每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线，垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器，且 n 的值至少为 2。

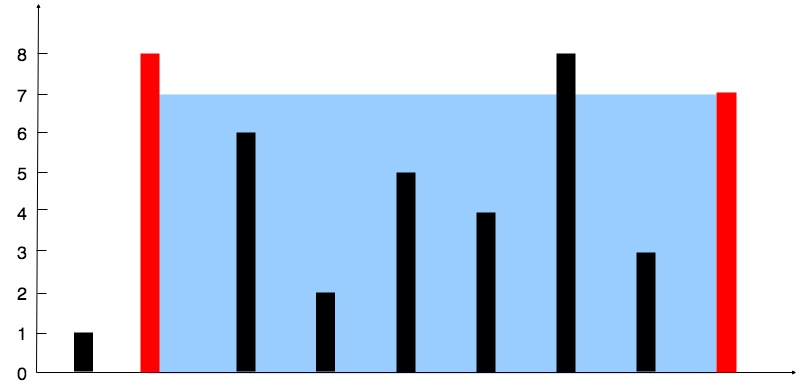
图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例:

　　输入: [1,8,6,2,5,4,8,3,7]

　　输出: 49

2、题解

2.1、解法一

class Solution:
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        left=0
        right=len(height)-1
        result=0
        while left<right:
            print(left,right)
            result=max(result,(right-left)*min(height[left],height[right]))
            # 移动短的。移动长的，总面积在减小；移动短的，总面积有可能增加
            if height[left]<height[right]:
                left+=1
            else:
                right-=1
    
        return result

2.2、解法二

class Solution:
    def maxArea(self, height):
        """
        :type height: List[int]
        :rtype: int
        """
        n = len(height)
        start = 0
        end = n-1
        maxarea = 0
        while(start<end):
            h = min(height[start], height[end])
            water = (end-start)*h
            if(water>maxarea):
                maxarea = water
            while(height[start]<=h and start<end): start+=1
            while(height[end]<=h and start<end): end-=1
        return maxarea