基于统计学习方法角度谈谈CRF
作者：白宁超
2016年8月2日13:59:46
【摘要】：条件随机场用于序列标注，数据分割等自然语言处理中，表现出很好的效果。在中文分词、中文人名识别和歧义消解等任务中都有应用。本文源于笔者做语句识别序列标注过程中，对条件随机场的了解，逐步研究基于自然语言处理方面的应用。成文主要源于自然语言处理、机器学习、统计学习方法和部分网上资料对CRF介绍的相关的相关，最后进行大量研究整理汇总成体系知识。文章布局如下：第一节介绍CRF相关的基础统计知识；第二节介绍基于自然语言角度的CRF介绍；第三节基于机器学习角度对CRF介绍，第四节基于统计学习角度对相关知识介绍；第五节对统计学习深度介绍CRF，可以作为了解内容。（本文原创，转载请注明出处：基于统计学习方法角度谈谈CRF。)
目录
【自然语言处理：漫步条件随机场系列文章（一）】：前戏：一起走进条件随机场
【自然语言处理：漫步条件随机场系列文章（二）】：基于自然语言处理角度谈谈CRF
【自然语言处理：漫步条件随机场系列文章（三）】：基于机器学习角度谈谈CRF
【自然语言处理：漫步条件随机场系列文章（四）】：基于统计学习角度谈谈CRF
【自然语言处理：漫步条件随机场系列文章（五）】：条件随机场知识扩展
引子
条件随机场（CRF）：是给定一组输入随机变量条件下，另一组输出随机变量的条件概率分布模型，其特点是假设输出随机变量构成马尔科夫随机场，条件随机场可用于不同预测问题，由输入序列对输出序列预测的判别式模型，形式为对数线性模型，其学习方法通常是极大似然估计。
1 条件随机场(CRF)的定义与形式
简单的说，条件随机场(CRF)类似于MRF，只不过CRF比MRF多了一个观察集合，或者说，CRF本质上就是给定了观察值集合的MRF。
条件随机场：设G=(V,E)是一个无向图，Y={Yv|v∈V}是以G中节点v为索引的随机变量Yv构成的集合。在给定X的条件下，如果每个随机变量Yv服从马尔可夫性，即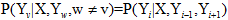
，则条件概率分布P(Y|X)就是一个条件随机场。上式中的w ~ v表示在图G=(V, E)中与节点v有边连接的所有节点，w≠v表示v以外的所有节点，Yv,Yu, Yw为w对节点v，u，w对应的随机变量。
线性链条件随机场：
设X = (X1, X2,..., Xn), Y = (Y1, Y2, ..., Yn)均为线性链表示的随机变量序列，若在给定随机变量序列X的条件下，随机变量序列Y的条件概率分布P(Y|X)构成条件随机场，即满足马尔可夫性(见本文最开始的“模型定义”部分)： P(Yi| X, Y1, ..., Yi-1, Yi+1, ...., Yn)= P(Yi | X, Yi-1, Yi+1) i= 1, 2, ..., n (在i=1和n时只考虑单边)，则称P(Y|X)为线性链条件随机场。
注意：在标注问题中，X表示输入观测序列，Y表示对应的输出标记序列或状态序列。
2 条件随机场的参数化形式
P(Y|X)为线性链条件随机场，则在随机变量X取值为x的条件下，随机变量Y取值为y的条件概率具有如下形式：
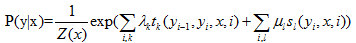
其中，
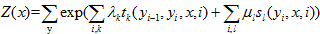
式中，tk和sl是特征函数，λk和μl是对应的权值。Z(x)是规范化因子，求和时在所有可能的输出序列上进行的。
通常：特征函数t和s取值是1或0，当满足特征条件取值1，反之取值0，条件随机场完全由特征函数t，s和对应的数值λ，μ确定。
注意：线性CRF也是对数性模型。
实例解析：
设有一个天气预测问题：输入观察序列（连续三天的天气情况）为X = (X1, X2, X3)，输出标记序列（每天对应天气热冷的预测）为 Y = (Y1, Y2, Y3)， Y1, Y2, Y3 的取值于y= {H, C},其中H表示天热，C表示天冷。假设特征tk,sl和对应的权值λk，μl如下：
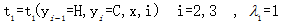
其中，上式代表着特征值为H的条件，即：yi-1= H, yi=C, x, i = 2, 3 时特征值取1。而特征值取0的条件被省略了。
PS：如果写全的话是这样：
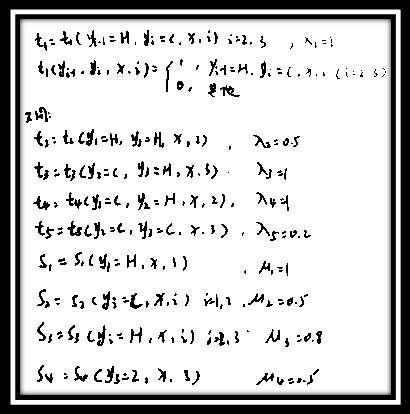
于是对给定的观测序列x，求标记序列为y =(y1, y2, y3) = (H, C, C),即第一天热，第二天第三天连续冷的非规范化条件概率（即没有除以规范化因子的条件概率）
实例分析：
由以上问题可知，观察序列是天数的集合，标记序列是对应天气热冷的集合，由此分析显然是随机条件场的编码问题，基于随机条件场，可以将上述情形转换为图形化形式分析，然后进行模型构建，算法实现，算法优化和结果分析即可。本节重点实现分析，图形表示，模型构建。
天气预测问题转化为图形表示如下：
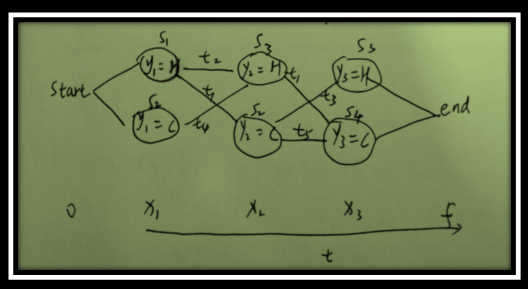
如图所示，横坐标x1，x2，x3分别对应天，是观察序列具备时序性，纵坐标是标记序列即可能隐藏的所有标记情况，start和end表示开始和结束状态（这点参照笔者Viterbi算法一节的介绍），其中t表示转移概率，t=0.5有具体权值的，标注转移概率是50%机会。X对应的s表示发射概率或者生产概率，显然，如上满足条件随机场，回顾下条件随机场模型，线性链条件随机场模型为：
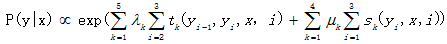
于是对给定的观测序列x，标记序列y=(H,C,C)的非规范化条件概率为
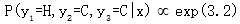
上式数值计算，参照已知条件和图形分析，很容易计算，这里具体计算过程省略。
3 条件随机场的简化形式
将局部特征转化为一个全局特征函数，可将CRF写成权值向量和特征向量的内积形式即是条件随机场的简化形式，具体参见如下笔记：
① 将转移特征和状态特征以及其数值用统一符号表示，设有K1个转移贴纸，K2个状态特征，K=K1+K2，记：
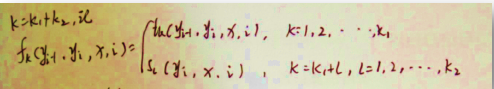
② 对转移状态各个位置i求和，记作：
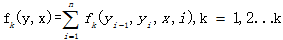
③ 用wk表示特征fk(y,x)的权值，即：
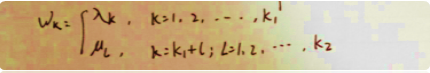
④ 于是，条件随机场可表示为
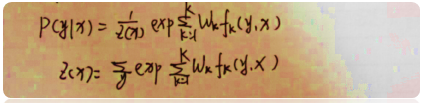
⑤ 以w表示权值向量，即
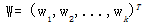
⑥ 以F(y, x)表示全局特征向量，即
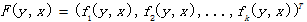
则条件随机场可以写成向量w与F(y, x)的内积的形势：
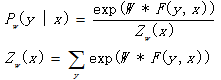
4 条件随机场预测算法
形式化描述： 条件随机场的预测问题是给定义条件随机场P(Y|X)和输入序列(观测序列)x，求条件概率最大的输出序列(标记序列)y*，即对观测序列进行标注。 条件随机场的预测算法是著名的维特比算法。
你对维特比算法是什么就有概念了吧，下面来看看其数学描述。维特比算法不做深入讲解，如果读者还不清楚，参考本人系列文章之揭秘马尔科夫模型系统文章，有专门章节详细介绍viterbi算法。
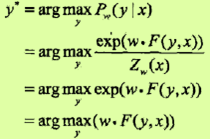
这里，路径表示标记序列，其中
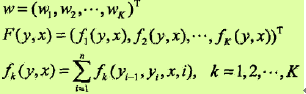
注意，这时只需计算非规范化概率，而不必计算概论，可以大大提高效率。
为了求解最优路径，将式写成如下形式：
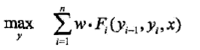
其中
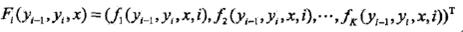
就是局部特征向量。
下面叙述维特比算法。
实例解析
用维特比算法求给定的输入序列(观测序列)x对应的输出序列(标记序列)y* = (y1*, y2*, y3*)；
解析：
1)第一步初始化：因为y1=1和y1=2是最初，所以就不用考虑转移的情况了(实际上也没有“表达从y0转移到y1的情况”的t函数(转移函数))，直接从状态函数(s函数中找)，发现，s1和s2分别对应y1=1和y1=2，说明y1=1和y1=2这个状态都是存在的，而s1和s2的权值分别是1和0.5，且上面列出的s函数们和t函数们值都为1，所以y1=1和y2=1的可能性分别是1和0.5。所以，到达y1的非规范化概率最大值为：δ1(1) = 1，δ1(2) = 0.5。
2)第二步递推：i=2(达第二处目的地集合{y2=1, y2=2})：首先是路线(仅说明到达y2=1的情况)：
上图可知，到达y2=1的路线有如下几条：
路线1：从y1=1出发 ----(经过t2)---->到达y2=1；
路线2：从y1=2出发 ----(经过t4)---->到达y2=1；
接着是状态(仅说明到达y2=1的情况)：
根据题目可知：i=2时的状态函数只有s2和s3，而y2=1对应的函数是s3
所以到达y2=1的非规范化概率最大值为：δ2(1) = max{1+λ2t2 + u3s3,0.5 + λ4t4 + u3s3}= 2.4
非规范化概率最大值的路径为： ψ2(1) = 1
δ2(2)同理。
i=3也一样（只不过对于δ3(1)中的u5s5，我认为应该是u3s3，先不说s3对应的是y3=1的情况，而且原题中根本没有s5函数）。
3)第三步终止：这步就简单了，在δ3(l)中δ3(1) = 4.3最大，所以y3中取1的可能性最大，即y3*=1。
4)第四步返回：然后反着推：
从y2的哪个值到y3可能性最大呢？在第二部已经解出：ψ3(1) = 2，即y2到达y3=1的路线中权值最大的是y2=2，即y2*=2。
同理，从y1=1到y2=2的可能性最大，即y1*=1。
5)就得到标记序列:*= (y1*, y2*, y3*)= (1, 2, 1)
5 参考文献
【1】 数学之美 吴军 著
【2】 机器学习 周志华 著
【3】 统计自然语言处理 宗成庆 著（第二版）
【4】 统计学习方法（191---208） 李航
【5】 知乎 网络资源
6 自然语言相关系列文章
【自然语言处理】：【NLP】揭秘马尔可夫模型神秘面纱系列文章
【自然语言处理】：【NLP】大数据之行，始于足下：谈谈语料库知多少
【自然语言处理】：【NLP】蓦然回首：谈谈学习模型的评估系列文章
【自然语言处理】：【NLP】快速了解什么是自然语言处理
【自然语言处理】：【NLP】自然语言处理在现实生活中运用
声明：关于此文各个篇章，本人采取梳理扼要，顺畅通明的写作手法。系统阅读相关书目和资料总结梳理而成，旨在技术分享，知识沉淀。在此感谢原著无私的将其汇聚成书，才得以引荐学习之用。其次，本人水平有限，权作知识理解积累之用，难免主观理解不当，造成读者不便，基于此类情况，望读者留言反馈，便于及时更正。本文原创，转载请注明出处：基于统计学习方法角度谈谈CRF。