| 我的GitHub | 我的博客 | 我的微信 | 我的邮箱 |
|---|---|---|---|
| baiqiantao | baiqiantao | bqt20094 | baiqiantao@sina.com |
目录
开篇词 (1讲)
开篇词 | 从今天起,跨过“数据结构与算法”这道坎
基础知识就像是一座大楼的地基,它决定了我们的技术高度。而要想快速做出点事情,前提条件一定是基础能力过硬,“内功”要到位。
为了由浅入深地带你学习,我把专栏分成四个递进的模块
- 入门篇:时间、空间复杂度分析
- 基础篇:涵盖了最基础、最常用的数据结构和算法
- 高级篇:不是那么常用的数据结构和算法
- 实战篇:通过实战部分串讲一下前面讲到的数据结构和算法
人生路上,我们会遇到很多的坎。跨过去,你就可以成长,跨不过去就是困难和停滞。而在后面很长的一段时间里,你都需要为这个困难买单。对于我们技术人来说,更是这样。
既然数据结构和算法这个坎,我们总归是要跨过去,为什么不是现在呢?
入门篇 (4讲)
01 | 为什么要学习数据结构和算法?
- 想要通关大厂面试,千万别让数据结构和算法拖了后腿
- 业务开发工程师,你真的愿意做一辈子 CRUD boy 吗?
- 不需要自己实现,并不代表什么都不需要了解。
- 在这些基础框架中,一般都揉和了很多基础数据结构和算法的设计思想。
- 掌握数据结构和算法,不管对于阅读框架源码,还是理解其背后的设计思想,都是非常有用的。
- 基础架构研发工程师,写出达到开源水平的框架才是你的目标!
- 对编程还有追求?不想被行业淘汰?那就不要只会写凑合能用的代码!
- 性能好坏起码是其中一个非常重要的评判标准
掌握了数据结构与算法,你看待问题的深度,解决问题的角度就会完全不一样。因为这样的你,就像是站在巨人的肩膀上,拿着生存利器行走世界。数据结构与算法,会为你的编程之路,甚至人生之路打开一扇通往新世界的大门。
02 | 如何抓住重点,系统高效地学习数据结构与算法?
什么是数据结构?什么是算法?
从广义上讲,数据结构就是指一组数据的存储结构。算法就是操作数据的一组方法。
从狭义上讲,是指某些著名的数据结构和算法,比如队列、栈、堆、二分查找、动态规划等。这些都是前人智慧的结晶,我们可以直接拿来用。我们要讲的这些经典数据结构和算法,都是前人从很多实际操作场景中抽象出来的,经过非常多的求证和检验,可以高效地帮助我们解决很多实际的开发问题。
数据结构和算法有什么关系呢?
数据结构和算法是相辅相成的。数据结构是为算法服务的,算法要作用在特定的数据结构之上。
数据结构是静态的,它只是组织数据的一种方式。如果不在它的基础上操作、构建算法,孤立存在的数据结构就是没用的。
学习这个专栏需要什么基础?
这个专栏不会像《算法导论》那样,里面有非常复杂的数学证明和推理。
对于每个概念和实现过程,我都会从实际场景出发,不仅教你“是什么”,还会教你“为什么”,并且告诉你遇到同类型问题应该“怎么做”。
学习的重点在什么地方?
首先要掌握一个数据结构与算法中最重要的概念——复杂度分析。
数据结构和算法解决的是如何更省、更快地存储和处理数据的问题,因此,我们就需要一个考量效率和资源消耗的方法,这就是复杂度分析方法。
20 个最常用的、最基础数据结构与算法
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
要学习它的“来历”、“自身的特点”、“适合解决的问题”以及“实际的应用场景”
一些可以让你事半功倍的学习技巧
- 边学边练,适度刷题
- 可以“适度”刷题,但一定不要浪费太多时间在刷题上。我们学习的目的还是掌握,然后应用。
- 多问、多思考、多互动
- 学习最好的方法是,找到几个人一起学习,一块儿讨论切磋,有问题及时寻求老师答疑。
- 打怪升级学习法
- 学习的过程中,我们碰到最大的问题就是,坚持不下来。
- 我们在枯燥的学习过程中,也可以给自己设立一个切实可行的目标
- 知识需要沉淀,不要想试图一下子掌握所有
- 学习知识的过程是反复迭代、不断沉淀的过程。
一张图,建议保存
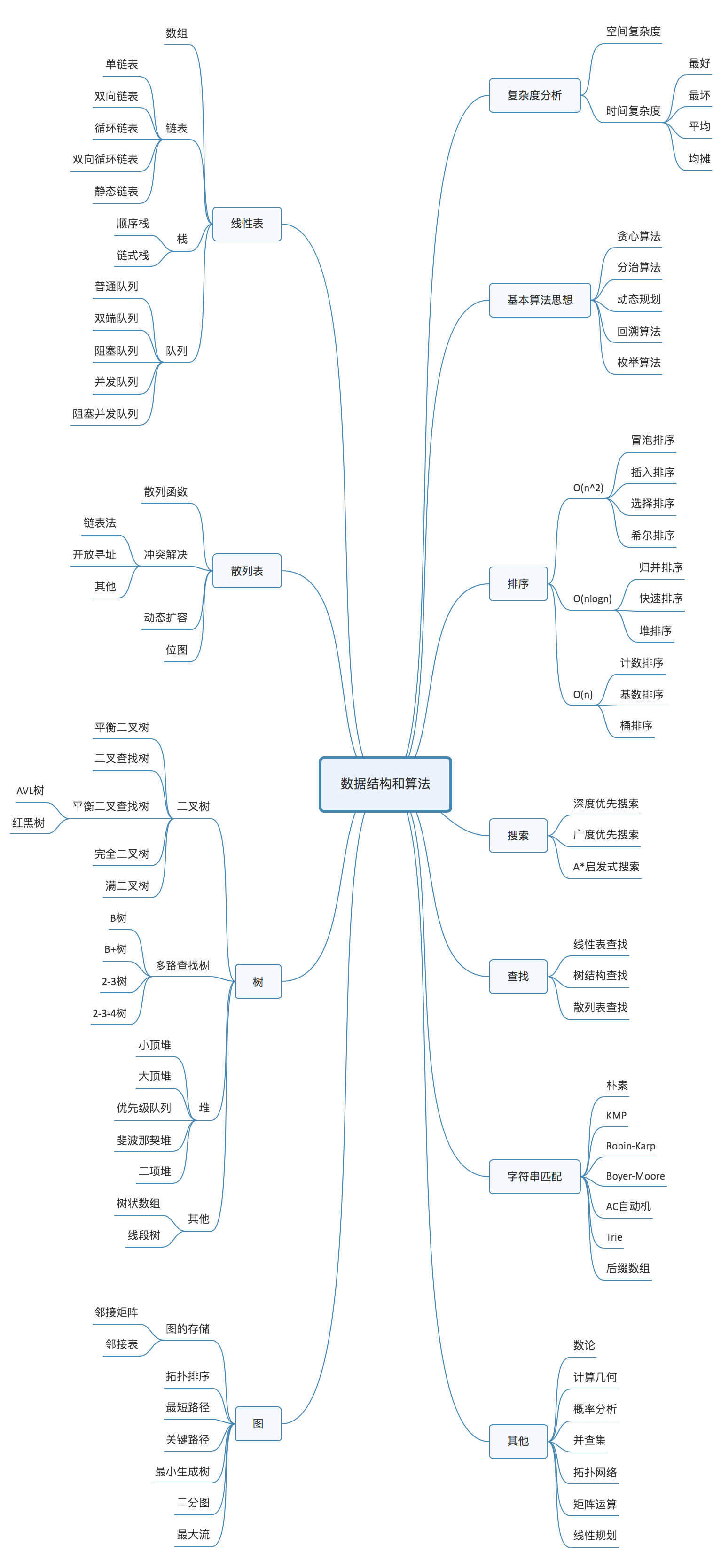
03 | 复杂度分析(上):如何分析、统计算法的执行效率和资源消耗?
复杂度分析是整个算法学习的精髓,只要掌握了它,数据结构和算法的内容基本上就掌握了一半。
为什么需要复杂度分析?
事后统计法的局限性
- 测试结果非常依赖测试环境
- 测试结果受数据规模的影响很大
我们需要一个不用具体的测试数据来测试,就可以粗略地估计算法的执行效率的方法。这就是时间、空间复杂度分析方法。
大 O 复杂度表示法
大 O 时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度(asymptotic time complexity),简称时间复杂度。
时间复杂度分析
- 只关注循环执行次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
几种常见时间复杂度实例分析

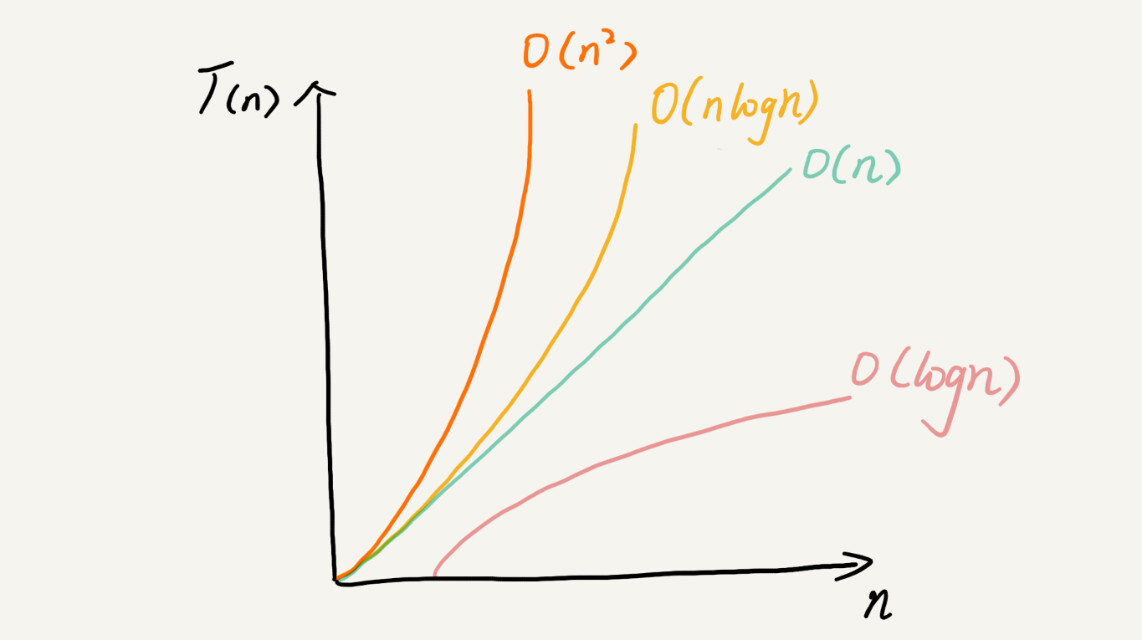
O(1)O(1)只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码- 一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)
O(logn)、O(nlogn)- 在采用大 O 标记复杂度的时候,可以忽略系数,即
O(Cf(n)) = O(f(n)) - 不管是以 2 为底、以 3 为底,还是以 10 为底,我们可以把所有对数阶的时间复杂度都记为
O(logn)。为什么呢?因为对数之间是可以互相转换的。
- 在采用大 O 标记复杂度的时候,可以忽略系数,即
O(m+n)、O(m*n)- 代码的复杂度由两个数据的规模来决定
空间复杂度分析
时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。类比一下,空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系。
我们常见的空间复杂度就是 O(1)、O(n)、O(n2),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。
内容小结
复杂度也叫渐进复杂度,包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系,可以粗略地表示,越高阶复杂度的算法,执行效率越低。常见的复杂度并不多,从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)。
04 | 复杂度分析(下):浅析最好、最坏、平均、均摊时间复杂度
- 最好、最坏情况时间复杂度
- 最好情况时间复杂度就是,在最理想的情况下,执行这段代码的时间复杂度。
- 最坏情况时间复杂度就是,在最糟糕的情况下,执行这段代码的时间复杂度。
- 平均情况时间复杂度
- 平均时间复杂度的全称应该叫
加权平均时间复杂度或者期望时间复杂度。
- 平均时间复杂度的全称应该叫
- 均摊时间复杂度
- 均摊时间复杂度就是一种特殊的平均时间复杂度
- 我们没必要花太多精力去区分它们。你最应该掌握的是它的分析方法,摊还分析。
2021-7-23