P1350 车的放置

题面

有下面这样的一个网格棋盘，(a,b,c,d) 表示了对应边长度，也就是对应格子数。

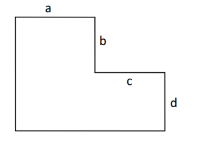
当 (a=b=c=d=2)时，对应下面这样一个棋盘：

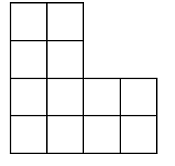
要在这个棋盘上放 (k) 个相互不攻击的车，也就是这 (k) 个车没有两个车在同一行，也没有两个车在同一列，问有多少种方案。

只需要输出答案 (mod100003)后的结果。

输入格式

共一行，五个非负整数 (a,b,c,d,k)

输出格式

包括一个正整数，为答案 (mod100003) 后的结果。

数据范围

(1≤a,b,c,d,k≤1000)
保证至少有一种可行方案。

输入样例：

2 2 2 2 2

输出样例：

38

题解

乘法原理，加法原理

将原来的图分成上下两块，分别在上半部分放(i)个，下半部分放(k-i)个，方案数之间是加法原理，因为两两之间没有关系

• 先考虑上半部分

若在上半部分放(i)个，则要从(b)行中选择(i)行来进行放置，是一个组合问题，即(C_{b}^{i})

再考虑列，因为车的前后顺序不同，方案也不同，所以是个排列问题，即(A_{a}^{i})

而这两者相互之间是影响的，所以应该是相乘的关系，即(C_{b}^{i})(A_{a}^{i})

• 再考虑下半部分

下半部分放(k-i)个，则要从(d)行中选择(k-i)来进行放置，是一个组合数的问题，即(C_{d}^{k-i})

再考虑列，同上的，排列的方案数应该是(A_{a+c-i}^{k-i})

内部是乘法原理，因为后面的结果会受到前面的影响

取模的时候，为了保险，还是+mod%mod吧

代码

#include<bits/stdc++.h>
using namespace std;
const int mod=1e5+3;
const int N=6000;
int fact[N],infact[N];
int a,b,c,d,k;
long long res;
int qmi(int a,int b)
{
	int ans=1;
	while(b)
	{
		if(b&1) ans=(long long) ans*a%mod;
		a=(long long)a*a%mod;
		b>>=1;
	}
	return ans;
}


void init()
{
	fact[0]=infact[0]=1;
	for(int i=1; i<4000; i++)
	{
		fact[i]=(long long)fact[i-1]*i%mod;
		infact[i]=(long long)infact[i-1]*qmi(i,mod-2)%mod;
	}
}


long long A(int a,int b)
{
	if(a<b) return 0;
	return (long long)fact[a]*infact[a-b]%mod;
}

long long C(int a,int b)
{
	if(a<b)return 0;
	return (long long)fact[a]*infact[a-b]%mod*infact[b]%mod;
}


int main()
{
	cin>>a>>b>>c>>d>>k;
	init();
	for(int i=0; i<=b; i++)
	{
		res=(res+(((long long)C(b,i)*A(a,i)%mod)*((long long)C(d,k-i)*A(a+c-i,k-i)%mod)%mod)+mod)%mod;
	}
	cout<<res<<endl;
}