P4799 [CEOI2015 Day2]世界冰球锦标赛

[Usaco2012 Open]Balanced Cow Subsets

题目描述

给出(N(1≤N≤20))个数(M(i)(1<=M(i)<=100,000,000))，在其中选若干个数，如果这几个数可以分成两个和相等的集合，那么方案数加1。

求有多少种选数的方案。

输入输出格式

输入格式：

第一行，两个正整数 (N) 和 (M(1 leq N leq 40,1 leq M leq 10^{18}))，表示比赛的个数和 Bobek 那家徒四壁的财产。

第二行，(N) 个以空格分隔的正整数，均不超过 (10^{16})，代表每场比赛门票的价格。

输出格式：

输出一行，表示方案的个数。由于 (N) 十分大，注意：答案 (le 2^{40})。

输入输出样例

输入样例#1：

4 
1 
2 
3 
4 

输出样例#1：

3 

思路

做法1

老夫写代码就一个词，暴力搜，咳咳

先说40分的暴力思路

考虑每个物品选还是不选就行，一个小小的剪枝

if(sum>M) return;

代码得分40分

#include<bits/stdc++.h>
using namespace std;
long long n,a[50];
long long M;
long long ans;
void dfs(int u,long long sum)
{
	if(sum>M)return ;
	if(u==n+1)
	{
		ans++;
		return ;
	}
	dfs(u+1,sum+a[u]);
	dfs(u+1,sum);
}
int main()
{
	cin>>n;
	cin>>M;
	for(int i=1; i<=n; i++)
		cin>>a[i];
	dfs(1,0);
	cout<<ans<<endl;
	return 0;
}

做法二

显然要折半搜索呀

下面引出主角——折半搜索（meet in the middle思想）

因为(Nleq40) (O(2^{40}))的爆搜一定会(TLE)，所以我们将NN分成两份

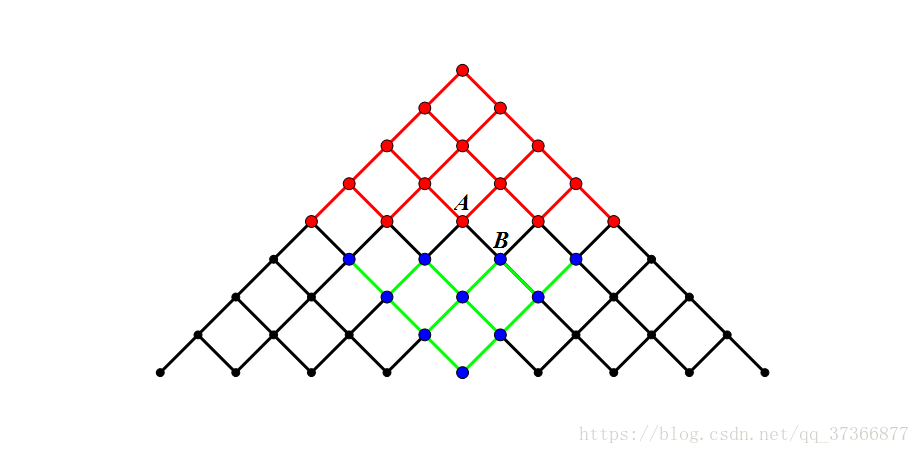
搜索(1)到(n/2)和(n/2+1)到(n)，让复杂度降到(O(2^{n/2+1}))组合答案的复杂度))。

画一个图（网上找的不错的图）理解一下为什么能降低复杂度

void dfs(int l,int r,long long sum,long long &cnt,long long suma[])
{
	if(sum>M)return ;
	if(l>r)
	{
		suma[++cnt]=sum;
		return ;
	}
	dfs(l+1,r,sum+a[l],cnt,suma);
	dfs(l+1,r,sum,cnt,suma);
}

将前一半的搜索状态存入(suma)数组，后一半存入(sumb)数组。

mid=n/2;
dfs(1,mid,0,cnta,suma);
dfs(mid+1,n,0,cntb,sumb);

一般(meet in the middle)的难点主要在于最后答案的组合统计。

我们可以现将(suma)或(sumb)数组(sort)，让其有序。

然后通过枚举另一个数组中的状态，来实现统计答案。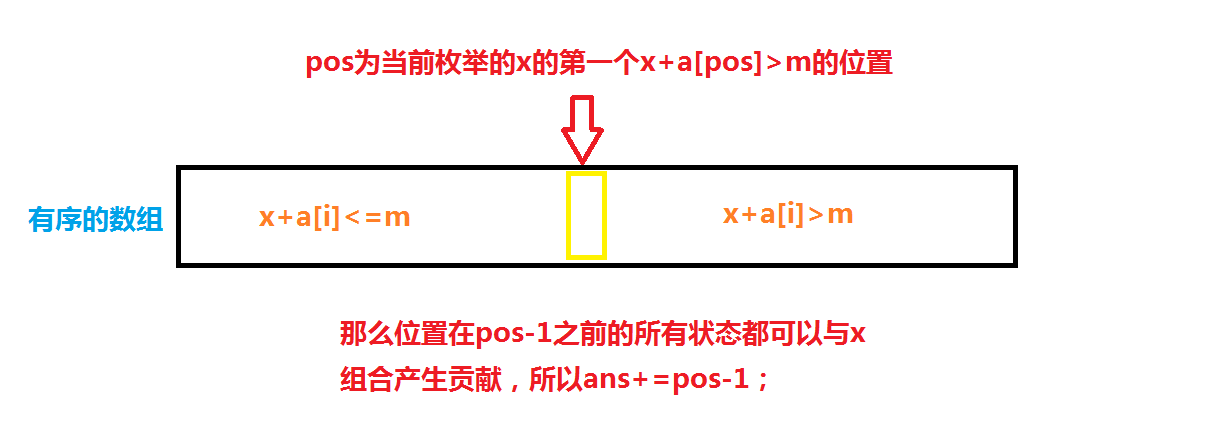

上述找(pos)的过程可以通过upper_bound()完成。

这里是找到第一个大于该数的位置

long long pos=upper_bound(suma+1,suma+1+cnta,M-sumb[i])-suma;

所以(1——pos-1)位置的(suma)都是满足条件的，所以有

ans+=pos-1;

啊喂，记得看数据范围呀,开long long

代码

#include<bits/stdc++.h>
using namespace std;
long long n,a[50];
long long M;
long long ans;
long long suma[2000000],sumb[2000000];
long long cnta,cntb;
void dfs(int l,int r,long long sum,long long &cnt,long long suma[])
{
	if(sum>M)return ;
	if(l>r)
	{
		suma[++cnt]=sum;
		return ;
	}
	dfs(l+1,r,sum+a[l],cnt,suma);
	dfs(l+1,r,sum,cnt,suma);
}
int main()
{
	cin>>n;
	cin>>M;
	for(int i=1; i<=n; i++)
		cin>>a[i];
	int mid=n/2;
	dfs(1,mid,0,cnta,suma);
	dfs(mid+1,n,0,cntb,sumb);
	sort(suma+1,suma+1+cnta);
	for(int i=1;i<=cntb;i++)
	{
		long long pos=upper_bound(suma+1,suma+1+cnta,M-sumb[i])-suma-1;
		ans+=pos;
	}
	cout<<ans<<endl;
	return 0;
}