1.二分法求方程根
二分法求根基于二分查找的思想。
比如求根号2的近似值,猜测它在1到2之间,则将1作为left,2作为right,反复二分比较f(mid)的平方与2的大小,直到(right-left)的精度eps控制在一定范围以内。
代码:
#include <iostream>
using namespace std;
const double eps = 1e-5;
double f(double x)
{
return x * x;
}
double calSqrt()
{
double left = 1, right = 2, mid;
while (right - left > eps)
{
mid = (left + right) / 2; //避免溢出 mid = left + (right - left)/2;
if (f(mid) > 2)
right = mid;
else
left = mid;
}
return mid;
}
int main()
{
cout << calSqrt();
return 0;
}
2.牛顿迭代法求方程根
例如求f(x)=0,画图如下,求方程根即求f(x)与x轴交点的值。假设这个点叫Xn好了。
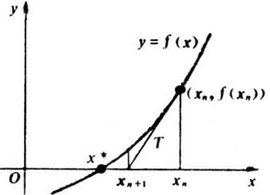
牛顿迭代法的思想是,首先取一个与Xn相近的点,假定为X0。
作X0在f(x)上的切线,切线与X轴相交于X1。注意此时X1比X0更接近我们最终要找的Xn。
按同样的方式,继续作X1对应的f(x)的切线,与X轴相交于X2。反复这样做,X轴交点就会越来越逼近Xn。这就是迭代的过程,预设的精度就是循环终止的条件。
既然是迭代,自然有迭代公式,我们要寻找Xn与Xn-1之间的关系。比如说就找X1与X0,其实就是X0对应的切线方程,令y=0。
切线方程
y = f(X0)+f'(X0)(x-X0)
令y = 0,得 X1 = X0-f(X0)/f'(X0)
所以也有
Xn = Xn-1-f(Xn-1)/f'(Xn-1)
举个例子,求根号6的近似值。
代码:
#include <iostream>
using namespace std;
const double eps = 1e-5;
double f(double x)
{
return x * x - 6;
}
double calSqrt()
{
double x_0 = 6 / 2;
double x_1 = x_0 - f(x_0) / (2 * x_0);
while ((x_0 - x_1) > eps)
{
x_0 = x_1;
x_1 = x_0 - f(x_0) / (2 * x_0);
}
return x_1;
}
int main()
{
cout << calSqrt();
return 0;
}
输出
2.44949