119.杨辉三角 II
描述
给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行。
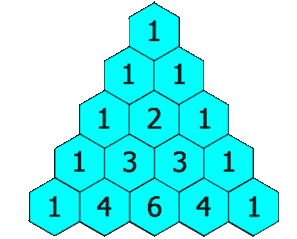
在杨辉三角中,每个数是它左上方和右上方的数的和。
示例
输入: 3
输出: [1,3,3,1]
进阶:
你可以优化你的算法到 O(k) 空间复杂度吗?
思路
不同于上一题, 这里我们仅仅需要得到的第 k 层的集合, 但只能使用 O(k) 的空间。 所以不能用前面二维数组的方式, 只能使用一维数组滚动计算。
在第一题里面, 我们知道, 帕斯卡三角的计算公式是:
A[k][n] = A[k-1][n-1] + A[k-1][n]。
假设现在数组存放的第 3 层的数据, [1, 3, 3, 1], 如果我们需要计算第 4 层的数据, 如果我们从前往后计算,譬如 A[4][2]= A[3][1] + A[3][2],也就是 4,但是因为只有一个数组,所以需要将 4 这个值覆盖到 2 这个位置,那么我们计算 A[4][3] 的时候就会出现问题了,因为这时候 A[3][2] 不是 3, 而是 4 了。
为了解决这个问题, 我们只能从后往前计算, 仍然是上面那个例子, 我们实现计算 A[4][3] = A[3][2] + A[3][3], 也就是 6, 我们将 6 直接覆盖到 3 这个位置, 但不会影响我们计算 A[4][2], 因为 A[4][2] = A[3][1] + A[3][2], 已经不会涉及到 3 这个位置了。
class Solution:
def getRow(self, rowIndex):
"""
:type rowIndex: int
:rtype: List[int]
"""
res = [1] * (rowIndex + 1)
for i in range(rowIndex + 1):
for j in range(i-1, 0, -1):
res[j] = res[j] + res[j-1]
return res
GitHub地址:https://github.com/protea-ban/LeetCode
