快速排序 两种partition实现

标签： 算法基础

---

1. 算法简介

　　快速排序，正如其名字一样，是排序算法中速度较快的一种排序，算法复杂度为(O(n*logn))。
　　排序过程中会打乱元素的相对位置，是不稳定排序。

　　算法思想：选定一个pivot，把元素分为两组，一组比pivot小，一组比pivot大，然后按照相同的方法处理这两组元素，是一个递归的过程。

　　算法核心是partition方法，即把元素分开两组的方法，每次把元素平均分到两边时，算法效率最高。相反，如果每次partition把元素完全分到一边，是最差情况，算法退化为(O(n^2))。

　　下面详细介绍两种partition方法。假设需要排序的数组为: 21, 34, 74, 3, 20, 2, 56, 46, 6。

2. partition1方法

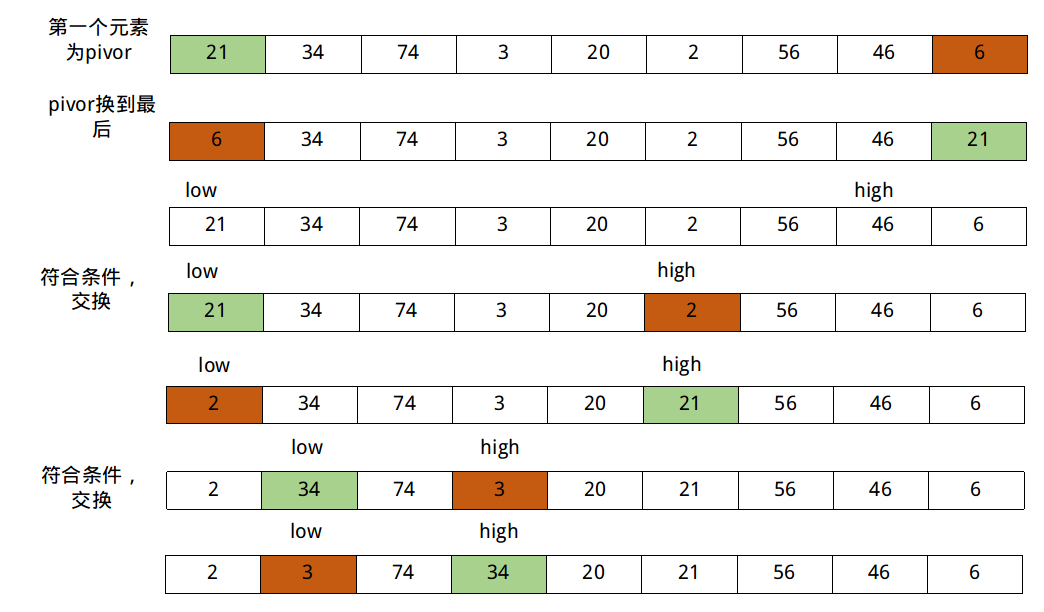
　　先把选定为pivot的元素放到最后，然后设定指针low和指针high，low指针左移，high指针右移，当两个指针相撞后停止移动。期间如果符合交换条件，两元素交换。最后把pivot元素放到中间。
　　这里选择数组第一个元素作为pivot。

代码：

/**
  * @arr 待排序的数组
  * @begin 需要partition的起始下标
  * @end 需要partition的末尾下标
  * @return 返回pivot所在位置下标
  */
int partition1(int arr[], int begin, int end) {
	int pivotIndex = begin;
	int pivot = arr[pivotIndex];
	swap(arr, pivotIndex, end);

	int low = begin;
	int high = end;

	while (low < high) {
		// 因为把pivot放在了最后，所以low指针先走
		while (low < high && arr[low] < pivot) low++; 
		while (low < high && arr[high] > pivot) high--;
		if(low < high) swap(arr, low, high);
	}

	swap(arr, low, end);
	return low;
}

3. partition2方法

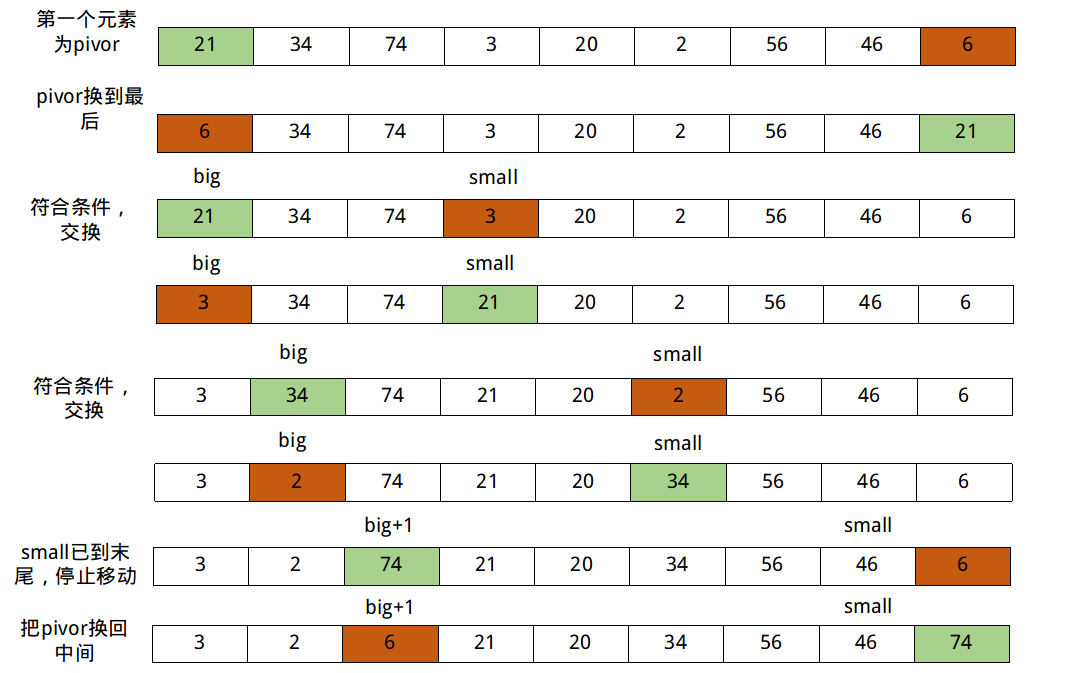
　　类似冒泡排序的思路，把比pivot大的元素“往下沉”，把比pivot小的元素“往上浮”。
　　

代码：

/**
  * @arr 待排序的数组
  * @begin 需要partition的起始下标
  * @end 需要partition的末尾下标
  * @return 返回pivot所在位置下标
  */
int partition2(int arr[], int begin, int end){
    int pivotIndex = begin;
    int pivot = arr[pivotIndex];
    swap(arr, pivotIndex, end);
   
    int big = begin - 1; // index of smaller element
    for (int small = begin; small <= end - 1; small++){
        // 遇到一个元素小于pivot
        if (arr[small] <= pivot){
            big++;
            swap(arr, big, small);
        }
    }
    swap(arr, big + 1, end);
    return big + 1;
}

4.快速排序代码

void quickSort(int[] arr, int begin, int end) {
	if (begin < end){
	    int p = partition1(arr, begin, end);
	    // int p = partition2(arr, begin, end);
	    quickSort(arr, begin, p - 1);
	    quickSort(arr, p + 1, end);
	}
}

public static void main(String []argc){
    int []array = {21, 34, 74, 3, 20, 2, 56, 46, 6};
    quickSort(array, 0, array.length - 1);
}

5. 算法优化

1. 在递归到规模比较小时，使用选择排序/插入排序代替。
2. 选取一个比较靠谱的pivot。（取first，取last，取middle，取三者的中）
3. 使用循环代替递归。