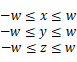1 向量
1.1 点-向量-二者关系
点:二维、三维空间一个点的坐标,描述位置。如a(ax, ay, az)
向量:二维、三维空间中向量描述原点到相对于某个点的位移移动,具有方向和长度(大小)属性。描述位移。如a(ax, ay, az)
向量大小:|v| = √(a2+b2+c2+…+n2),表示向量的长度。
向量标准化:vnorm = v/|v| , v不能为零向量,如下图,对a(ax, ay)归一化运算:![clip_image001[4] clip_image001[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011314696-1722381893.png)
1-1. 归一化(标准化)
关系:向量描述位移,包括相对位置。点描述位置。把向量比喻为一个箭头,头是点,尾是原点,整个向量就是点相对于原点的偏移。
1.2 零向量与负向量
零向量:[0,0,…,0],是一个没有位移、没有方向的向量。加性单位元。
负向量:任何向量都有负向量。-[x, y, z] = [-x, -y, -z]。加性逆元。几何解释:改变方向
1.3 向量的加法、减法运算
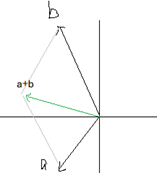
加法几何解释一:三角形法则
1-2. 加法三角形法则
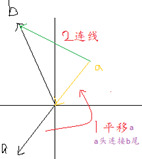
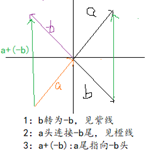
加法几何解释二:平行四边形法则
平移图1-1中绿色线至a与b的交点(不再移动a),组成平行四边形,求半角向量,如下图:
1-3. 平半角向量
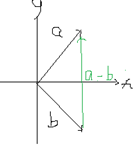
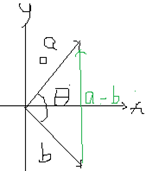
减法几何解释:一个点到另一个点的向量。
减法:先把向量转为负向量再做加法。本职还是加法,继续使用三角形法则
1-4. 右图对左图减法的详细拆解
1.4 标量与向量乘法:
放大k倍:k · a = k · (ax, ay, az) = (kax, kay, kaz)
1.5 向量与向量乘法-点积
点积结果返回标量值.
//unity vector3点积计算 public static float Dot(Vector3 lhs, Vector3 rhs) { return (float) ( (double) lhs.x * (double) rhs.x + (double) lhs.y * (double) rhs.y + (double) lhs.z * (double) rhs.z ); }
点积的几何解释一:角度
点积等于向量大小与向量的夹角:(同一平面)
a·b = |a| |b| cos θ
θ = arccos(a·b / (|a| b|) )
如果a、b是单位向量,则分母为1,简化:
θ = arccos(a·b)
1-5. a、b向量夹角
a·b > 0,θ∈[0°, 90°)
a·b = 0,θ = 90°
a·b > 0,θ∈(90°, 180°]
Unity实际应用方位判断
//判断a、b方位。求b在a的前后左右相对位置: Transform a, b; Vector3 diffVec = a.position – b.position; float front_back = Vector3.Dot(a.position.forward, diffVec); float left_right = Vector3.Dot(a.position.right, diffVec); if(front_back > 0) 前方 else 后方 if(left_right > 0) 右方 else 左方
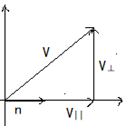
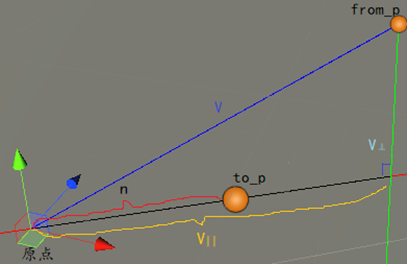
点积的几何解释二:投影向量
1-6. 向量投影
V可以拆分:V⊥是垂直向量,V||是投影向量
V = V⊥ + V||
如何求投影向量V||?
用三角函数求V||的模:
带入计算求得向量V||
最后也可方便求V⊥
Unity的Vector3.Project分析:
public static Vector3 Project(Vector3 vector, Vector3 onNormal) { //pow(onNormal, 2) float num1 = Vector3.Dot(onNormal, onNormal); if ((double) num1 < (double) Mathf.Epsilon) return Vector3.zero; float num2 = Vector3.Dot(vector, onNormal); return new Vector3( onNormal.x * num2 / num1, onNormal.y * num2 / num1, onNormal.z * num2 / num1 ); }
实战如何用Vector3.Project算出V||
1-6. 事例
求投影向量和垂直向量,以及投影交点坐标:
public Transform m_from_p;
//一般为法线
public Transform m_to_p;
//相对于from_p和to_p而言
public Transform m_origin_p;
private Vector3 m_projects = Vector3.zero;
void Update()
{
//warning: 要统一坐标空间
//Vector3 toP_foDirect = m_to_p.InverseTransformDirection(m_from_p.position - m_origin_p.position);
Vector3 toP_foDirect = m_from_p.position - m_origin_p.position;
Vector3 toP_toDirect = m_to_p.position - m_origin_p.position;
//求出投影向量 V_ii
m_projects = Vector3.Project(toP_foDirect, toP_toDirect);
//from到原点连线
Debug.DrawLine(m_origin_p.position, m_from_p.position, Color.blue);
//绘制投影向量线
Debug.DrawLine(m_origin_p.position, m_origin_p.position + m_projects, Color.black);
//投影点坐标, 对project_P求模可以知道from_p到to_p所在轴的最短距离
Vector3 project_P = m_origin_p.position + m_projects;//float minDis = project_P.magnitude;
//垂直向量
Vector3 V_T = project_P - m_from_p.position;
//绘制垂直向量线
Debug.DrawLine(m_from_p.position, m_from_p.position + V_T.normalized * 100f, Color.green);
}如
果一个向量v在自身投影,就是v·v = vx2 + vy2 + vz2 = |v|2,继而可以求出v的模
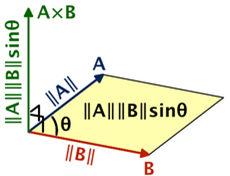
1.6 向量与向量乘法-叉积
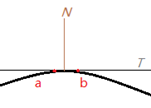
向量a与向量b的叉积结果向量n,n垂直于向量a与b组成的平面,可把其看作平面法线。
1-7. 叉乘示意图
1-8. 叉积计算公式
几何解释一:平行四边形面积
几何解释二:顺时针和逆时针方向
a = (x1, y1, z1), b = (x2, y2, z2); //a x b = (y1 * z2 - y2 * z1, z1 * x2 - x1 * z2, x1 * y2 - y1 * x2) double ans = (y1 * z2 - y2 * z1)+(z1 * x2 - x1 * z2)+( x1 * y2 - y1 * x2) if(ans>0) cout<<"逆时针"<<endl; if(ans<0) cout<<"顺时针"<<endl; if(ans==0) cout<<"共线"<<endl;
几何dot、cross:求点到点的角度
// 通过 Dot、Cross 结合获取到 a 到 b, b 到 a 的不同夹角 private void GetAngle(Vector3 a, Vector3 b) {
/*ab叉积求得时针方向,点积求得*/
Vector3 c = Vector3.Cross(a, b);
float angle = Vector3.Angle(a, b);//只能返回[0°, 180°]
// b 到 a 的夹角
float sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(a.normalized, b.normalized)));
float signed_angle = angle * sign;
Debug.Log("b -> a :" + signed_angle);
// a 到 b 的夹角
sign = Mathf.Sign(Vector3.Dot(c.normalized, Vector3.Cross(b.normalized, a.normalized)));
signed_angle = angle * sign;
Debug.Log("a -> b :" + signed_angle);
}shader中叉积计算写法
//shader中叉积计算写法float crossProduct = a.yzx * b.zxy - a.zxy * b.yzx;2 矩阵
行矩阵
列矩阵
对角矩阵
也是方块矩阵,行与列相同
除了对角线以外的元素都为0,称为方块矩阵
单位矩阵-一种特殊的对角矩阵
默认用 I 表示单位矩阵
对角线元素全为1,其余元素都为0
任何矩阵与单位矩阵相乘,结果任为其本身
转置矩阵---转置运算
-
MijT = Mji
-
矩阵的行变为列,列变为行
-
(A·B)T = BT·AT,具有反向串接各矩阵
逆矩阵
-
必须为方阵才有逆矩阵行列相等(n=m)
-
M-1·M = I //必须满足
-
(M-1)-1 = M
-
I-1 = I //单位矩阵的逆矩阵=自身
-
(MT)-1 = (M-1)T //转置矩阵的逆矩阵等于逆矩阵的转置
-
(A·B·C)-1 = C-1 ·B-1·A-1//反向串接各矩阵
正交矩阵
-
M·MT = MT·M = I
-
任何正交矩阵行列式值:|A|= 1或 -1
-

线性变换
缩放、旋转、平移
只需要改变单位矩阵对角线元素值,(其中w分量为1)===> 目标矩阵(行矩阵)·S(q)
把M3x3看作缩放旋转,t3x1看作平移,1为w分量
将一个矩阵进行缩放、旋转、平移的复合变换先后顺序不一样,其结果也不一样。绝大多数情况下都是采用前述顺序。
矩阵的几何意义
为了进一步研究多元方程组,将多元方程组的系数组合在一个矩形数表,形成了矩阵。例如把三元方程组转化为三阶矩阵
例如,已知子坐标空间C的3个坐标轴在父坐标空间P下的表示xc, yc, zc,以及其原点位置Oc。当给定一个子坐标空间中的一点Ac = (a,b,c),按照下面4个步骤求出Ac在父坐标空间下的位置。
1从坐标空间原点开始Oc
2向x轴方向移动x个单位:Oc + axc
3向y轴方向移动y个单位:Oc + axc + byc
4向z轴方向移动z个单位:Oc + axc + byc + czc
Ap = Oc + axc +byc + czc
= (xoc, yoc ,zoc) + a(xxc, yxc, zxc) + b(xyc , yyc, zyc) + c(xzc, yzc, zzc)
透视投影矩阵:
横纵比:摄像机的ViewPortRect中的W和H属性决定着Game视图横纵比
计算某一点是否在裁剪区域内,只需将该点与![]() ,由观察空间变换到裁剪空间。
,由观察空间变换到裁剪空间。
注意此时的W分量,可能<0为负数。如果一个点在视锥体内,必须满足
正交投影矩阵
那么将顶点带入该矩阵相乘:
判断条件如下
法线变换
有MA->B 顶点变换矩阵, N是法线,T是切线, G是法线变换矩阵
根据点积性质变换前垂直:(TA)T·NA = 0
变换后也应该垂直:(TA->B)T·NA->B = 0
切线公式:TB = (MA->B · TA)T
切线变换步骤:
TB · NB = (MA->B · TA)T ·(G · NA)
= (TA)T ·MA->BT·(G · NA) = (TA)T · NA ·(MA->BT·G)
由于TAT·NA = 0
如果(MA->BT·G) = 0,G = (MA->B-1)T
如果MA->B是正交矩阵,变换包含旋转和系数k统一缩放,MA->B的逆转置矩阵 = (MA->BT)-1 = (MA->B-1)T
如果MA->B是正交矩阵,变换包含旋转和系数k统一缩放,则(MA->B)-1=![]() , 简要推导如下
, 简要推导如下
设MA->B = k·M(M为正交矩阵),
等式左边:(MA->B)-1=(K·M)-1 = 1/k · M-1
等式右边:1/K2 · (K·M)T = 1/k2 · k · MT = 1/K · M-1
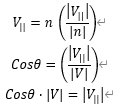
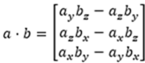
![clip_image012[4] clip_image012[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011319988-1851277813.png)
![clip_image013[4] clip_image013[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011320470-1762296936.jpg)
![clip_image014[4] clip_image014[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011320948-621881887.png)
![clip_image015[4] clip_image015[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011321411-1210310394.png)
![clip_image016[4] clip_image016[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011321878-1015122552.png)
![clip_image017[4] clip_image017[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011322359-31342737.png)
![clip_image018[4] clip_image018[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011322824-755480781.png)
![clip_image019[4] clip_image019[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011323368-1262025871.png)
![clip_image020[4] clip_image020[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011323851-527915459.png)
![clip_image021[4] clip_image021[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011324303-1954413085.png)
![clip_image022[4] clip_image022[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011324785-244803131.png)
![clip_image024[4] clip_image024[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011325261-714795684.png)
![clip_image028[4] clip_image028[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011326186-83206810.png)
![clip_image030[6] clip_image030[6]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011327078-1369475577.png)
![clip_image034[4] clip_image034[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011327983-731482179.png)
![clip_image030[7] clip_image030[7]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011328430-657859497.png)
![clip_image036[4] clip_image036[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011329363-1716579989.png)
![clip_image038[6] clip_image038[6]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011330339-1090725151.png)
![clip_image038[7] clip_image038[7]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011331286-189059943.png)
![clip_image048[4] clip_image048[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011333672-208842827.png)
![clip_image052[4] clip_image052[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011334638-441651048.png)
![clip_image054[4] clip_image054[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011335139-1987000879.png)
![clip_image056[6] clip_image056[6]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011335593-2002507893.png)
![clip_image064[4] clip_image064[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011337557-2066639362.png)
![clip_image066[4] clip_image066[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011338044-15971364.png)
![clip_image068[4] clip_image068[4]](https://img2018.cnblogs.com/blog/1692664/201910/1692664-20191009011338537-108723341.png)