一、概率定义
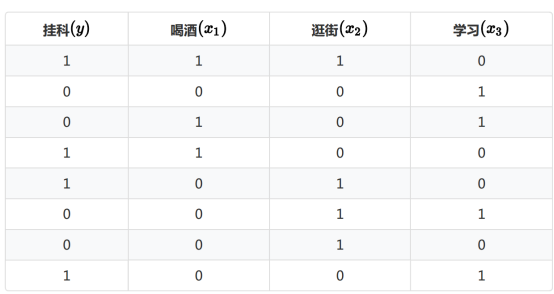
条件概率：假设A=挂科，B=喝酒，C=逛街，D=学习
P(AꓵB)：A和B同时发生
P(A｜B) :在已知B条件的情况下，A发生的概率
已知是否喝酒，挂科的概率
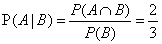喝酒并且挂科的概率
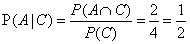逛街并挂科的概率
学习并且挂科的概率
二、贝叶斯公式推导：
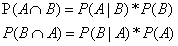
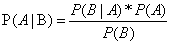……贝叶斯公式
三、应用
问题：假如一个学生没有喝酒(x1=0)、没有逛街(x2=0)、学习了(x3=1)，是否会挂科
根据贝叶斯公式可得：
分两种情况考虑
Y=1:
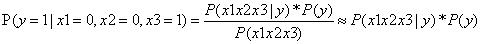……①
Y=0:
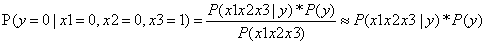……②
马尔可夫假设：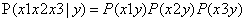 
所以上述①可推导为：
……③
②式可推导为：
……④
由③可得：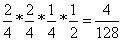
由④可得：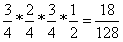
因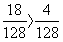
，故得结论，没有喝酒、没有逛街、学习了，不挂科的概率要高很多
例2 由下表的训练数据学习一个朴素贝叶斯分类器并确定
的类标记y，表中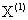
，
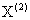为特征，取值的集合分别为
,
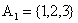,Y为类标记,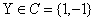
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| |
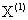1 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
3 |
3 |
3 |
3 |
3 |
| |
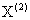S |
M |
M |
S |
S |
S |
M |
M |
L |
L |
L |
M |
M |
L |
L |
|
Y |
-1 |
-1 |
1 |
1 |
-1 |
-1 |
-1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
-1 |
首先计算出如下概率：
，
，
，
，
，
,
，
,
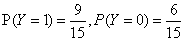
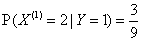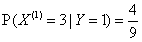
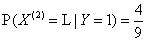
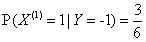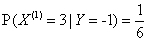
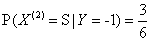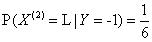
对于给定的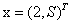
计算：
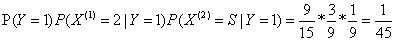
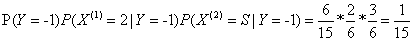
因为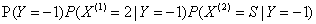
比较大，所以Y=-1
例2 问题同上，按照拉普拉斯平滑估计概率，取γ=1
为了解决零概率的问题，法国数学家拉普拉斯最早提出用加1的方法估计没有出现过的现象的概率，所以加法平滑也叫做拉普拉斯平滑。
假定训练样本很大时，每个分量x的计数加1造成的估计概率变化可以忽略不计，但可以方便有效的避免零概率问题。
利用拉普拉斯平滑概率重新计算概率
，
,
，
,
,
,
,
,
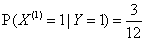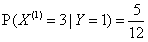
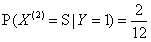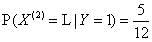
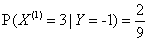
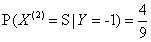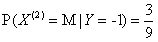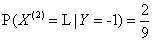
对于给定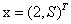
的计算：
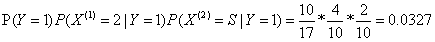
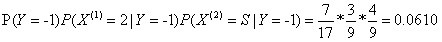
因为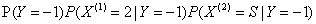
比较大，所以Y=-1