Ordinary Least Square 最小二乘法
提到最小二乘法要先提到拟合，拟合（Fitting）是数值分析（Numerical Analysis）的基础工具之一，拟合中最简单的是一元函数（function of one variable）拟合，一元函数拟合（即二维平面）分为直线拟合（一元一次函数，比如Y=aX+b）和曲线拟合（一元高次函数，比如Y=aX^2+bX+c），一元函数拟合中最简单的是直线拟合，直线拟合是找到一条直线尽可能穿过所有的点，注意这里是尽可能，因为只要超过2个点，就有可能发生直线不能精确穿过所有点的情况，这时确定直线的原则有很多种，最小二乘法就是其中的一种，当直线不能穿过点时产生误差（点和直线的距离），最小二乘法的原则就是让所有点的误差的平方和最小；
最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。
直线拟合（线性回归）过程如下图：
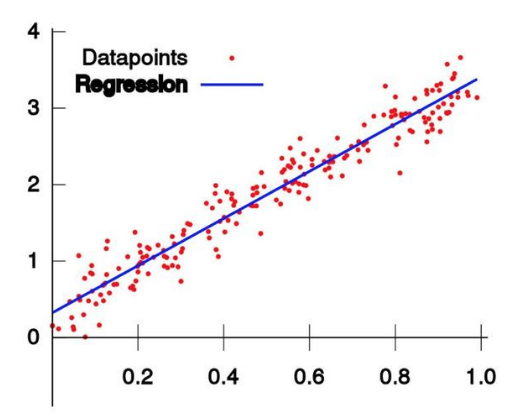
来看标准定义：
对给定数据点集合 
，在取定的函数类 
中，求 
，使误差的平方和 
最小， 
。从几何意义上讲，就是寻求与给定点集
的距离平方和为最小的曲线y=p(x)。函数p(x)称为拟合函数或最小二乘解，求拟合函数p(x)的方法称为曲线拟合的最小二乘法。
假设直线方程为
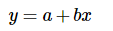
则误差为
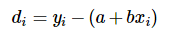
其中di表示(xi, yi)点的误差
所有误差的平方和为
这是一个2次函数，2次函数曲线如图：
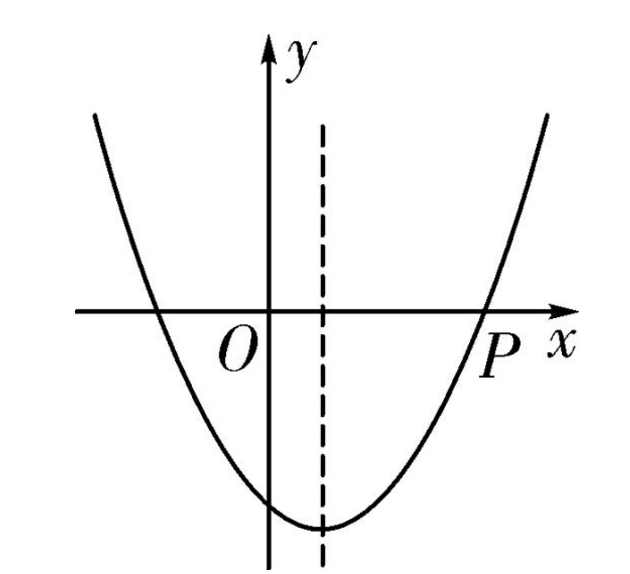
2次函数中D的最小值位于导数等于0的点，所以计算D对a和b的两个偏导数为0即可得到两个关于a和b的方程，
最终计算得出a和b的计算公式为：
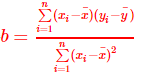
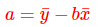
公式推导过程详见 https://www.cnblogs.com/paiandlu/p/7843236.html