1、 概述
Trie树,又称字典树,单词查找树或者前缀树,是一种用于快速检索的多叉树结构,如英文字母的字典树是一个26叉树,数字的字典树是一个10叉树。
Trie一词来自retrieve,发音为/tri:/ “tree”,也有人读为/traɪ/ “try”。
Trie树可以利用字符串的公共前缀来节约存储空间。如下图所示,该trie树用10个节点保存了6个字符串pool、prize、preview、prepare、produce、progress
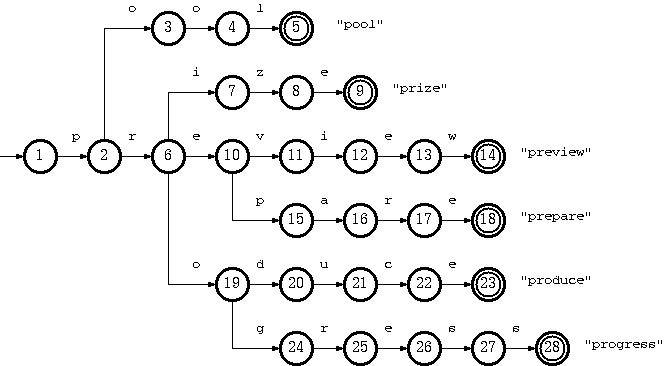
在该trie树中,字符串preview,prepare公共前缀是“pre”,因此可以只存储一份“pre”以节省空间。当然,如果系统中存在大量字符串且这些字符串基本没有公共前缀,则相应的trie树将非常消耗内存,这也是trie树的一个缺点。
Trie树的基本性质可以归纳为:
(1)根结点不包含字符,除根节点意外每个结点只包含一个字符。
(2)从根结点到某一个结点,路径上经过的字符连接起来,为该结点对应的字符串。
(3)每个结点的所有子结点包含的字符串不相同。
注意:每个结点可以有没有或者一个或者多个字结点,叶子结点没有子结点
2、数据结构表示
/** * 定义字典树的数据结构 * c 当前节点值 * isLeaf 是否是叶子结点 * children 孩子,key是孩子结点值,value是孩子结点的下一个字典树 * */ class TrieNode { char c; boolean isLeaf; HashMap<Character,TrieNode> children = new HashMap<Character,TrieNode>(); public TrieNode(char c){ this.c = c; } public TrieNode() {} }
3、Trie字典树查找
利用children HashMap,key是结点值,value是子结点
/** * 查找 返回最后的字符 * @param word * @return */ public TrieNode searchNode(String word){ HashMap<Character,TrieNode> children = root.children; TrieNode t = null;// 临时结点 // 遍历字符串word的每个字符 for(int i = 0;i<word.length();i++){ char c = word.charAt(i); if(!children.containsKey(c)){ return null; }else{ t = children.get(c); children = t.children; } }
// 返回最后一个结点,若空word不存在,若非空,并且是叶子结点则存在 return t; }
对返回的t进行判断, 返回最后一个结点,若空word不存在,若非空,并且是叶子结点则存在
/** * 查找是否存在 word字符 * @param word * @return */ public boolean search(String word){ TrieNode t= searchNode(word); // t.c 是字符串word最后一个结点值 return t!=null && t.isLeaf; }
查找前缀字符
/** * 查找前缀字符 * @param prefix * @return */ public boolean startsWith(String prefix) { return searchNode(prefix) != null; }
4、Trie字典树的插入
/** * 插入 * @param word */ public void insert(String word){ HashMap<Character,TrieNode> childern = root.children; for(int i=0;i< word.length();i++){ char c = word.charAt(i); TrieNode t = null; // 孩子结点中包括了 c 字符 if(childern.containsKey(c)){ t = childern.get(c);// c字符所在结点的 子字典树,进入下一个字典树 }else{ t = new TrieNode(c);// 不存在的时候新建结点 childern.put(c,t);// key value } childern = t.children;// 字典树的 孩子结点 if(i == word.length() - 1){ // 插入是叶子结点的时候 t.isLeaf = true; } } }
再说明下children
root
root.val 是结点值
root.children 的Key 是 root结点的孩子结点
root.children 的value 和 root.children中的Key一一对应,表示value的孩子结点
5、Trie字典树的删除
这个时间复杂度比较多
判断是否可以删除
定义parent child两个结点
当parent的孩子数量 > 1个 并且child的孩子有且只有一个的时候,将parent对于的这个孩子child删除
这里利用上面的searchNode,从下向上对word的子串进行判断
但是这里有个问题,举个例子好说:我们需要删除“pool”,但是“poo”在字典树也是合法的字符,我这样的程序也将“poo”进行了删除,如果定义一个计数器,比较好,当计数器为0的时候进行删除
/** * 删除 * 删除的是word这个字符串,首先要找到word和其他字符串的公共前缀,从最后一个公共前缀开始删除,结点 * 值为 null * @param word */ public void delete(String word){ boolean flag = search(word); if(flag==false){ System.out.println("不存在该字符串:"+word); return; } HashMap<Character,TrieNode> childern = root.children; TrieNode child = null;// 定义子结点 for(int i=word.length();i>=1 ;i--){ String subWord = word.substring(0,i); TrieNode parent = searchNode(subWord); if(child!=null && parent.children.size() !=1 && child.children.size()==1){ // 删除孩子结点 parent.children.remove(child.c); System.out.println("删除成功:"+word); return; }else{ child = parent; } } }
6、字典树的层次输出
利用二叉树层次遍历的思想
定义ArrayList或者队列,每次讲该层结点放到队列中,并删除父结点
public void printTrie(){ HashMap<Character,TrieNode> children = null; int size = 0; ArrayList<TrieNode> tree = new ArrayList<TrieNode>(); tree.add(root); while(tree.size()!=0){ size = tree.size(); for(int i =0;i<size;i++){ children = tree.get(0).children; tree.remove(0); // 把children中 value的值都放入到 tree中 if(children == null) break; for(TrieNode tN:children.values()){ tree.add(tN); System.out.print(tN.c +" "); } System.out.print("\"); } System.out.println(); } } }
上面程序对该层的元素进行了输出,
以“” 为分割部分的字符表示其父结点在:左上最近的结点
但是当某层出现单个字符的时候不能够很好的表示
同时,输出的时候发现每一层的最后一个结点是空,表示不理解
上面例子输出结果:
p
r o
e o i o
v p g d z l
i a
u e \
e
e c \
w e s e
\s \
最后s字符判断父结点出错,因为结点左侧过多的空的时候,只输出一个“”,但是为什么输出一个“”,我不理解,不知道哪里处理错误
全部程序

package twotree; import java.util.ArrayList; import java.util.HashMap; /** * 定义字典树的数据结构 * c 当前节点值 * isLeaf 是否是叶子结点 * children 孩子,key是孩子结点值,value是孩子结点的下一个字典树 * */ class TrieNode { char c; boolean isLeaf; HashMap<Character,TrieNode> children = new HashMap<Character,TrieNode>(); public TrieNode(char c){ this.c = c; } public TrieNode() {} } class Trie{ private TrieNode root = null; public Trie(){ root = new TrieNode(); } /** * 删除 * 删除的是word这个字符串,首先要找到word和其他字符串的公共前缀,从最后一个公共前缀开始删除,结点 * 值为 null * @param word */ public void delete(String word){ boolean flag = search(word); if(flag==false){ System.out.println("不存在该字符串:"+word); return; } HashMap<Character,TrieNode> childern = root.children; TrieNode child = null;// 定义子结点 for(int i=word.length();i>=1 ;i--){ String subWord = word.substring(0,i); TrieNode parent = searchNode(subWord); if(child!=null && parent.children.size() !=1 && child.children.size()==1){ // 删除孩子结点 parent.children.remove(child.c); System.out.println("删除成功:"+word); return; }else{ child = parent; } } } /** * 插入 * @param word */ public void insert(String word){ HashMap<Character,TrieNode> childern = root.children; for(int i=0;i< word.length();i++){ char c = word.charAt(i); TrieNode t = null; // 孩子结点中包括了 c 字符 if(childern.containsKey(c)){ t = childern.get(c);// c字符所在结点的 子字典树 }else{ t = new TrieNode(c);// 不存在的时候新建结点 childern.put(c,t);// key value } childern = t.children;// 字典树的 孩子结点 if(i == word.length() - 1){ // 插入是叶子结点的时候 t.isLeaf = true; } } } /** * 查找 返回最后的字符 * @param word * @return */ public TrieNode searchNode(String word){ HashMap<Character,TrieNode> children = root.children; TrieNode t = null;// 临时结点 // 遍历字符串word的每个字符 for(int i = 0;i<word.length();i++){ char c = word.charAt(i); if(!children.containsKey(c)){ return null; }else{ t = children.get(c); children = t.children; } } // 返回最后一个结点,若空word不存在,若非空,并且是叶子结点则存在 return t; } /** * 查找是否存在 word字符 * @param word * @return */ public boolean search(String word){ TrieNode t= searchNode(word); // t.c 是字符串word最后一个结点值 return t!=null && t.isLeaf; } /** * 查找前缀字符 * @param prefix * @return */ public boolean startsWith(String prefix) { return searchNode(prefix) != null; } public void printTrie(){ HashMap<Character,TrieNode> children = null; int size = 0; ArrayList<TrieNode> tree = new ArrayList<TrieNode>(); tree.add(root); while(tree.size()!=0){ size = tree.size(); for(int i =0;i<size;i++){ children = tree.get(0).children; tree.remove(0); // 把children中 value的值都放入到 tree中 if(children == null) break; for(TrieNode tN:children.values()){ tree.add(tN); System.out.print(tN.c +" "); } System.out.print("\"); } System.out.println(); } } } public class TrieTest { public static void main(String[] args){ Trie trie = new Trie(); // pool、prize、preview、prepare、produce、progress System.out.println(" insert"); trie.insert("pool"); trie.insert("prize"); trie.insert("preview"); trie.insert("prepare"); trie.insert("produce"); //trie.insert("produces"); trie.insert("progress"); System.out.println(" printTrie"); trie.printTrie(); System.out.println(" search"); System.out.println(trie.search("pool")); System.out.println(trie.search("produce")); System.out.println(trie.search("pop")); System.out.println(" searchNode"); System.out.println(trie.searchNode("pop") == null); System.out.println(trie.searchNode("pop")); System.out.println(trie.searchNode("produce") == null); System.out.println(trie.searchNode("produce").c); System.out.println(" startsWith"); System.out.println(trie.startsWith("pre")); System.out.println(trie.startsWith("hello")); System.out.println(trie.startsWith("pop")); System.out.println(" delete"); trie.delete("pool"); System.out.println(" printTrie"); trie.printTrie(); trie.delete("produce"); System.out.println(" printTrie"); trie.printTrie(); } }
输出结果

insert printTrie p r o e o i o v p g d z l i a u e \ e e c \ w e s e \s \ search true true false searchNode true null false e startsWith true false false delete 删除成功:pool printTrie p r e o i v p g d z i a u e e e c \ w e s e \s \ 删除成功:produce printTrie p r e o i v p g z i a e e e \ w e s \s
7、 Trie树的应用
Trie是一种非常简单高效的数据结构,但有大量的应用实例。
(1) 字符串检索
事先将已知的一些字符串(字典)的有关信息保存到trie树里,查找另外一些未知字符串是否出现过或者出现频率。
举例:
@ 给出N 个单词组成的熟词表,以及一篇全用小写英文书写的文章,请你按最早出现的顺序写出所有不在熟词表中的生词。
@ 给出一个词典,其中的单词为不良单词。单词均为小写字母。再给出一段文本,文本的每一行也由小写字母构成。判断文本中是否含有任何不良单词。例如,若rob是不良单词,那么文本problem含有不良单词。
(2)字符串最长公共前缀
Trie树利用多个字符串的公共前缀来节省存储空间,反之,当我们把大量字符串存储到一棵trie树上时,我们可以快速得到某些字符串的公共前缀。
举例:
@ 给出N 个小写英文字母串,以及Q 个询问,即询问某两个串的最长公共前缀的长度是多少?
解决方案:首先对所有的串建立其对应的字母树。此时发现,对于两个串的最长公共前缀的长度即它们所在结点的公共祖先个数,于是,问题就转化为了离线(Offline)的最近公共祖先(Least Common Ancestor,简称LCA)问题。
而最近公共祖先问题同样是一个经典问题,可以用下面几种方法:
1. 利用并查集(Disjoint Set),可以采用采用经典的Tarjan 算法;
2. 求出字母树的欧拉序列(Euler Sequence )后,就可以转为经典的最小值查询(Range Minimum Query,简称RMQ)问题了;
(3)排序
Trie树是一棵多叉树,只要先序遍历整棵树,输出相应的字符串便是按字典序排序的结果。
举例:
@ 给你N 个互不相同的仅由一个单词构成的英文名,让你将它们按字典序从小到大排序输出。
(4) 作为其他数据结构和算法的辅助结构
如后缀树,AC自动机等
8、 Trie树复杂度分析
(1) 插入、查找的时间复杂度均为O(N),其中N为字符串长度。
(2) 空间复杂度是26^n级别的,非常庞大(可采用双数组实现改善)。
9、 总结
Trie树是一种非常重要的数据结构,它在信息检索,字符串匹配等领域有广泛的应用,同时,它也是很多算法和复杂数据结构的基础,如后缀树,AC自动机等。
参考1:http://dongxicheng.org/structure/trietree/
参考2:http://linux.thai.net/~thep/datrie/datrie.html#Ref_Fredkin1960
