自己开发了一个股票智能分析软件,功能很强大,需要的点击下面的链接获取:
https://www.cnblogs.com/bclshuai/p/11380657.html
1.1 梯度下降法
1.1.1 简介
定义:梯度下降法是定义目标函数,通过误差反向传播的方法对模型参数进行调整,使得目标函数值最小,不再增长,则认为找到了一组参数,构造了模型。梯度下降法沿着误差下降速度最快的方向调整参数,一般是目标函数对某个参数的偏导数乘以步长来调整参数,最后使得误差收敛于最小值。这种方法适合在特征个数非常多,训练实例非常多,内存无法满足要求的时候使用。
梯度下降法考虑的问题
(1)步长:在梯度下降中一个重要的参数是步长,超参数学习率的值决定了步长的大小。如果学习率太小,必须经过多次迭代,算法才能收敛,这是非常耗时的。如果学习率太大,你将跳过收敛点。
(2)局部收敛点。并不是所有的损失函数看起来都像一个规则的碗。它们可能是洞,山脊,高原和各种 不规则的地形,使它们收敛到最小值非常的困难。
1.1.2三种梯度下降法比较
|
批量梯度 |
每次运算采用全部的数据集,运算量大,速度慢,收敛于最优解,容易陷入局部最优解。 |
|
随机梯度 |
随机选取训练集中的一个样本进行训练,运算量小,速度快,由于随机性,损失函数忽高忽低,不规则, 在最优解附件跳动。无法收敛于最优解。可以采用步长由大到小的方法实现优化。 |
|
小批量梯度 |
使用K个小批量样本子集,计算每个样本子集的损失函数,在求 平均值,用这个平均值去调整参数,利用了计算机的并行能力,一次计算了K个子集,运算量比随机梯度大,比批量梯度小,比随机梯度训练效果好,更接近最优解。可以采用变步长实现优化。 |
批量梯度参数迭代公式,对所有训练集N计算
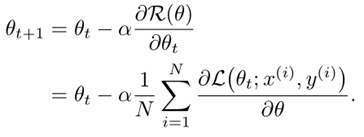
批量梯度算法的迭代过程如下:
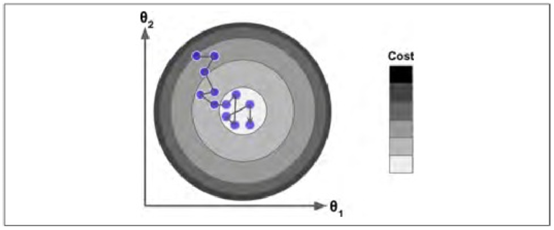
随机梯度参数迭代公式,选取小批量子集进行计算

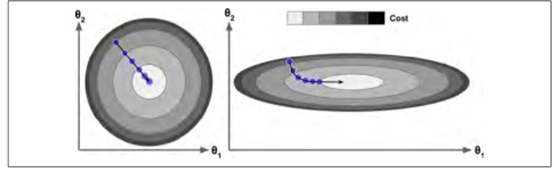
随机梯度下降法的迭代过程如下图所示,
小批量梯度下降法参数迭代公式
