这个算法可以用来解决分组,合并等问题。
代码

1 public static int MAXN = 10010; 2 // 作为承载并查集的数组 3 public static int []f = new int[MAXN]; 4 // 初始化并查集 5 public static void init() { 6 for (int i = 1; i < MAXN; i++) { 7 f[i] = i; 8 } 9 } 10 11 // 并查集状态压缩 12 public static int findFather(int x) { 13 // 下面进行求根(最顶端的那个点) 14 int a = x; 15 while (x != f[x]) { 16 x = f[x]; 17 } 18 19 // 下面进行状态压缩 20 while (a != f[a]) { 21 int z = a; 22 a = f[a]; 23 f[z] = x; 24 } 25 return x; 26 } 27 28 // 合并 29 public static void union(int a, int b) { 30 a = findFather(a); 31 b = findFather(b); 32 // 如果两个点的根节点不一样,就进行合,可以防止双向 33 // 1 2 , 2 1会被除以成一样 34 if(a != b) { 35 f[b] = a; 36 } 37 }
解释一下各部分代码的作用
先来看一个例子
有6个点(1,2,3,4,5,6),5条边。
第一条边
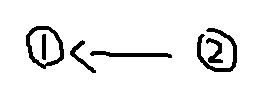
这时候,由原本1,2这两个点都指向自己(初始化init(),所有的节点都指向自己,比如f[2] = 2,f[1] = 1)
但是出现了一条边,需要2指向1,通过union(1, 2),使得2指向了1,f[2] = 1。
第二条边

本来应该和第一条边的处理一样,使得f[3] = 2,但是因为findFather()方法(findFather会一直往上“寻根”,)中,
有状态压缩的存在,使得f[3] = 1(为什么要这么处理呢?,因为判断点是否是同一组,是通过他们的根来判断的,
而且还能简化寻根这个过程,所以状态压缩一次,可以为后面findFather()寻根,判断点是否是一组节省时间)。

第四条边
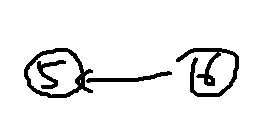
第五条边

状态压缩之后
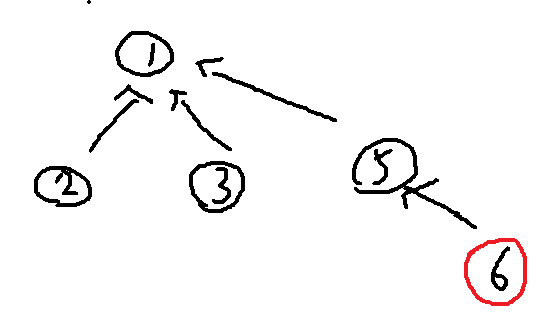
注意6这个点,如果不发生findFather()寻根,它是不会指向1的。
来看个例题
题输入n,m,k。表示有n个节点1-n,接下来输入m行,表示两个节点的相连,
再输入k行数字,每行表示删除一个节点,及与节点相连的边,然后输出剩下的节点
还需要连接几次,才能让让所有的点,连通。每次删除一个节点之后,要让所有点
恢复(啥意思呢?,比如,第一次删除了1,立马让其恢复,不能影响第二次删除2,
删除2的时候,1节点及其对应的连接还在)。
思路:可以使用并查集来解决分块问题,也可以使用深搜来解决。

1 import java.util.ArrayList; 2 import java.util.HashSet; 3 import java.util.Scanner; 4 import java.util.Set; 5 6 public class Main { 7 public static int MAXN; 8 public static int []f; 9 // 初始化 10 public static void init() { 11 for (int i = 1; i < MAXN; i++) { 12 f[i] = i; 13 } 14 } 15 16 // 寻根 并状态压缩 17 public static int findFather(int x) { 18 int a = x; 19 // 寻根 20 while (x != f[x]){ 21 x = f[x]; 22 } 23 // 状态压缩 24 while (a != f[a]) { 25 int z = a; 26 a = f[a]; 27 f[z] = x; 28 } 29 return x; 30 } 31 32 // 合并 33 public static void union(int a, int b) { 34 a = findFather(a); 35 b = findFather(b); 36 // 防止双向 37 if (a != b) { 38 f[b] = a; 39 } 40 } 41 42 public static void main(String[] args) { 43 Scanner sc = new Scanner(System.in); 44 int n, m , k; 45 n = sc.nextInt(); 46 m = sc.nextInt(); 47 k = sc.nextInt(); 48 int []A = new int[m + 1]; 49 int []B = new int[m + 1]; 50 for (int i = 0; i < m; i++) { 51 A[i] = sc.nextInt(); 52 B[i] = sc.nextInt(); 53 } 54 int tempSc, tempRoot; 55 MAXN = n + 1; 56 f = new int[MAXN]; 57 while (k > 0) { 58 tempSc = sc.nextInt(); 59 // 这里采用set来进行分块,当然也可以使用通过根来判断块的个数 60 61 // 初始化 62 init(); 63 64 for (int i = 0; i < m; i++) { 65 // 当前策略为B指向A 66 int tempA = findFather(A[i]); 67 int tempB = findFather(B[i]); 68 // 避开指向tempSc 69 if (tempA != tempB && tempA != tempSc && tempB != tempSc) { 70 f[tempB] = tempA; 71 } 72 } 73 int sum = 0; 74 for (int i = 1; i <= n; i++) { 75 if (f[i] == i) { 76 sum++; 77 } 78 } 79 System.out.println(sum - 2); 80 k--; 81 } 82 } 83 }
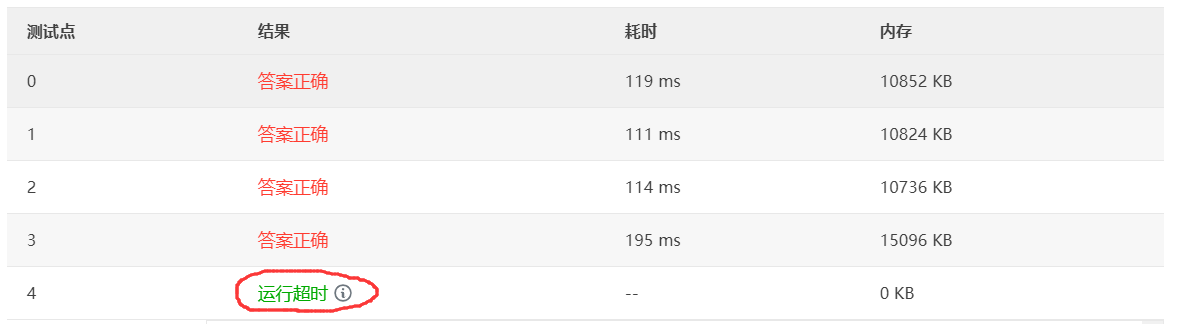
PAT好像对Java不友好,改成C就OK了。
