最小生成树

参考大神博客

      原理什么的直接看大神博客吧，我这里只做一个记录。
最小生成树
Kruskal思想
      将边通过边权进行升序排序，每次选取最小的边（贪心），如果当前的边,
属于另外一组，则将其加入到另外一组，如果属于任何一组，则自成一组。
（算法能成立的核心是，排序 + 贪心 + 并查集合并）
（1）连接两个点，花费一定是最小的。
（2）两条边合并，花费也是最小的。
（3）各个点连通一定n-1条边实现的。

Prim思想
      额，思想也是和Kruskal一样，只是实现很不一样。
（1）从任一节点出发，寻找与之距离最小的点now，并且记录这个距离。（与之
不相连的点，设为无穷大，例题代码没有设，做个标记）
（2）接下来寻找与now距离最小的点...重复直到图连通。

例子

HDU1233还是畅通工程

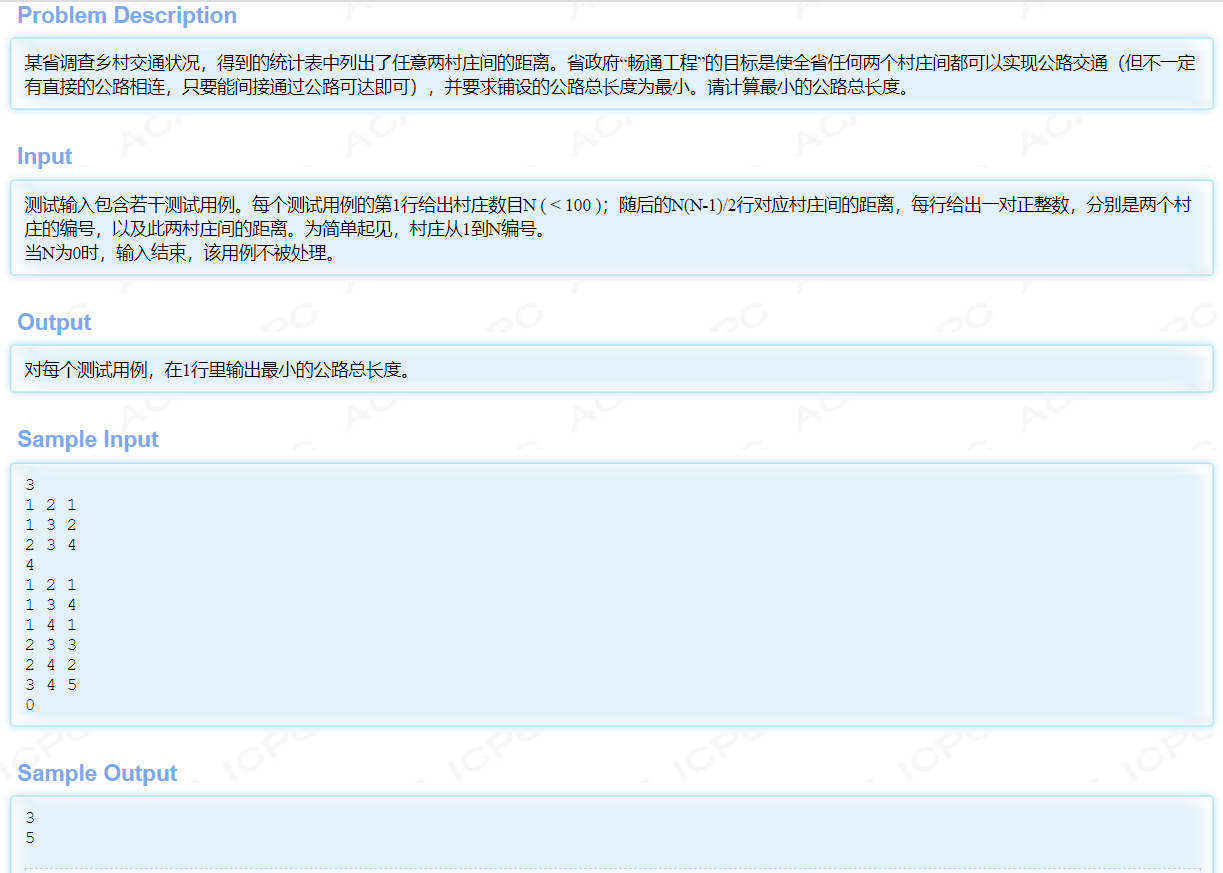
kruskal代码

#include<iostream>
#include<algorithm>
#include<stdio.h>
using namespace std;

int f[110] = {0};
int N, m;

struct edge {
	int u, v , weight;
}pp[6000];

// 重载 
bool cmp(edge e1, edge e2) {
	return e1.weight < e2.weight;
}

// 初始化
void init() {
	for (int i = 1; i <= N; i++) {
		f[i] = i;
	}
}

// 寻根 
int findFather(int x) {
	while (x != f[x]){
		x = f[x];
	}
	return x;
}

// 合并
//int Union(int a, int b) {
//	int fa = findFather(a);
//	int fb = findFather(b);
//	// 如果这两个点不属于一组 
//	if (fa != fb) {
//		f[fb] = fa;
//	}
//}

// 克鲁斯卡尔算法
int kruskal() {
	sort(pp, pp + N, cmp);
	// 初始化 
	init();
	int sum = 0;
	for (int i = 0; i < m; i++) {
		int fa = findFather(pp[i].u);
		int fb = findFather(pp[i].v);
		// 如果这两个点不属于一组 
		if (fa != fb) {
			f[fb] = fa;
			sum += pp[i].weight;
		}
	} 
	return sum;
}
int main()
{
    while (scanf("%d",&N) && N) {
    	m = N * (N - 1) / 2;
    	for (int i = 0; i < m; i++) {
    		scanf("%d%d%d",&pp[i].u, &pp[i].v , &pp[i].weight);
		}
		printf("%d
",kruskal());
	
//		for (int i = 0; i < m; i++) {
//			cout<<pp[i].u<<" "<<pp[i].v<<" "<<pp[i].weight<<endl;
//		}
	} 
} 

prim代码

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
int map[110][110] = {};
int vis[110] = {0};
int dis[110] = {0};
int n, m;
int max1 = 999999;
// 普利姆算法
int prim() {
	// 记录初始时，1到其他点的距离（当然也可以不选择1） 
	for (int i = 1; i <= n; i++) {
		dis[i] = map[1][i];
		vis[i] = false;
	}
	// 从1出发，标记其已访问 
	vis[1] = true;
	dis[1] = 0;
	// 表示当前操作到哪里了 
	int now = 1, sum = 0;
	// 循环 n - 1次 
	for (int i = 2; i <= n; i++) {
		int min1 = max1;
		for (int j = 1; j <= n; j++) {
			// 寻找最小边 (这里注意了，因为这个题，有 n * (n - 1) /2 表示任意两个点都有连接)
			// 所以不用考虑初始值为零的问题
			// 但是一般的题目还是要考虑的 
			if (vis[j] == false && dis[j] < min1){
				min1 = dis[j];
				// 寻找到的最小边 
				now = j; 
			}
		}
		// 这样表示当前节点 到达不了其他节点 
		// 这题可以不考虑，因为题目有很多边 
		if (min1 == max1) break;
		// 使得到达的节点标记已经访问 
		vis[now] = true;
		sum += min1;
		for (int j = 1; j <= n; j++) {
			// 将与now相连的节点的距离更新到dis中
			// 下一次就是找与now相连的节点了 
			if (vis[j] == false && dis[j] > map[now][j] ) {
				dis[j] = map[now][j];
			}
		}
	}
	return sum;
} 
int main()
{
	while ( scanf("%d",&n) && n) {
		m = n * (n - 1) / 2;
		int u, v, weight;
		for (int i = 0; i < m; i++) {
			scanf("%d%d%d", &u, &v, &weight);
			// 记录双向边 
			map[u][v] = map[v][u] = weight;
		}
		printf("%d
",prim());
	}
}