(5)归并排序
递归代码, 代码来自
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
//当只有一个元素的时候,返回
if (arr.length < 2) {
//此时分成了只有一个元素的数组,
//System.out.println( arr[0]);
return arr;
}
//向下取整
int middle = (int) Math.floor(arr.length / 2);
//一分为二
//左边部分
int[] left = Arrays.copyOfRange(arr, 0, middle);
//右边部分
int[] right = Arrays.copyOfRange(arr, middle, arr.length);
//将左边和右边,分别“重复”进行sort这个操作之后,合并(merge中排序)
return merge( sort( left ), sort( right ) );
//归并的第一个核心思想,分治进行合并
}
protected int[] merge(int[] left, int[] right) {
//装两个数组的新数组
int[] result = new int[left.length + right.length];
int i = 0;
//新的数组,下面进行的操作就是,依次挑选两数组种较小的开头元素(挑完就去掉那个元素),
//按顺序放入新数组
//这里有一个前提,就是这两个数组都已经排序好了(为什么?因为其中的一个数组,也是通过两个均只有一个元素的数组,进行如下排序得来的)
while (left.length > 0 && right.length > 0) {
//如果左数组第一个元素小于右数组的第一个元素
if (left[0] <= right[0]) {
//每次将left的第一个数组元素赋值给result
result[i++] = left[0];
//然后left得到“去掉“第一个元素的新数组
left = Arrays.copyOfRange(left, 1, left.length);
} else {
//如果左数组第一个元素大小于右数组的第一个元素
//每次将right的第一个数组元素赋值给result
result[i++] = right[0];
//然后right得到“去掉“第一个元素的新数组
right = Arrays.copyOfRange(right, 1, right.length);
}
//这样就解释了归并排序的另一核心思想,排序
//新数组每次挑选两个数组中较小的开头元素(挑选完之后,那个数组去掉被挑选的数,然后让下一个数成为开头元素)
//这样导致新数组有序(两个数组中的元素全部放到了新数组中,这些元素有序的放在了新数组中)
}
//后面收尾工作,因为上面的比较中,可能有一个数组有所剩余
//原因: 一个数组中的元素都比另外一个数组中的元素大(极端例子)
while (left.length > 0) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
}
while (right.length > 0) {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
return result;
}
优质代码, 代码来自
static void merge(int[] arr, int start, int end) {
if (start == end) return;
int mid = (start + end) / 2;
merge(arr, start, mid);
merge(arr, mid + 1, end);
int[] temp = new int[end - start + 1];
int i = start, j = mid + 1, k = 0;
while(i <= mid && j <= end)
temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++];
while(i <= mid)
temp[k++] = arr[i++];
while(j <= end)
temp[k++] = arr[j++];
//System.arraycopy(temp, 0, arr, start, end - start + 1);
// 下面代码和上面代码实现的是一样的
for (int i1 = 0; i1 < temp.length; i1++) {
arr[start + i1] = temp[i1];
}
}
(7)堆排序
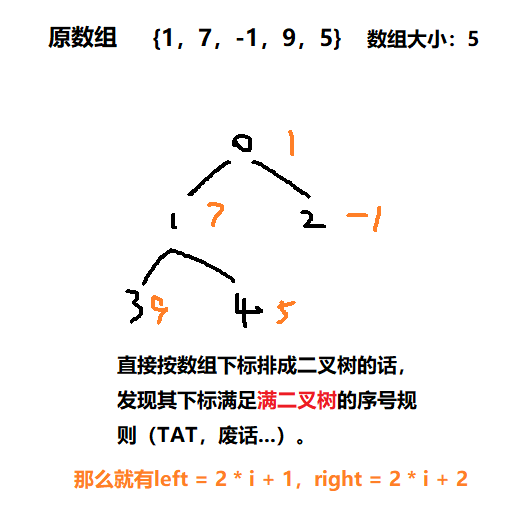
三个核心思想,
(1)构造大根堆 buildMaxHeap
// 构造大根堆
// 这里最“起码”能将最大的数字上浮至堆顶,
public void buildMaxHeap(int[] a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
maxHeapify(a, i, heapSize);
}
}
为什么说“起码”能将最大的数字上浮至堆顶,又为什么是 heapSize/2 : 0 (从heapSize / 2 到 0
看完后面应该知道为什么是heapSize / 2 : 0, 而不是 0 : heapSize / 2)

注意画红线的点,maxHeapify会有解释。
从heapSize / 2 到 0,兼顾了所有节点(没划红线的不就没有兼顾吗),往下看maxHeapify操作。
(2)maxHeapify
// 当前index和它的左右子树进行的操作。
// (1)挑出,当前左节点left(left = 2 * i + 1)指向的数字,当前右节点right( right = 2 * i + 2)指向的数字,中较大的,
// 与largest( = index )进行交换
// (2)然后让largest( = max(left,right))指向的元素和其左右子树进行交换,重复(1),直到当前指向没有左右子树,或者左右子树都比当前指向的数字小
public void maxHeapify(int[] a, int i, int heapSize) {
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
// (1)挑出,当前左节点l指向的数字,当前右节点r指向的数字,中较大的,
// 与largest进行交换
// (2)然后让largest指向的元素和heapSize指向的元素进行比较
// 进行(1),直到
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if (r < heapSize && a[r] > a[largest]) {
largest = r;
}
if (largest != i) {
swap(a, i, largest);
maxHeapify(a, largest, heapSize);
}
}
先来看一个简单的下沉,上浮。
当前指向了4,4会和左右节点进行比较,一直进行下沉(满足条件一直下沉),数字大的节点会上浮。
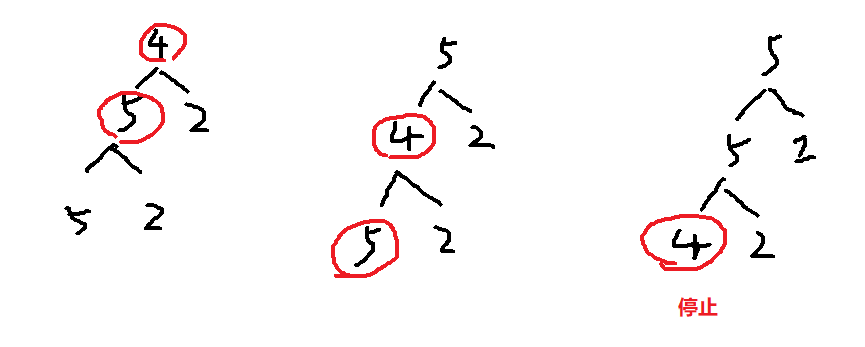
解释

这样一来,如果满足条件,就会一直下沉,数字大的上浮。
这两张图应该就能说明兼顾了叶子节点(因为当前节点会和左右节点进行比较)。
(3)heapSort 使用一次(1) 循环使用(2)
将堆顶数字和heapSize指向的数字(从代码中能看出它是在变的)进行交换。首先从(1)(2)知道了堆顶的数字一定的最大的(这里讲的是升序)。
交换之后,最大的数字(没排序的数字里面算最大)就放在了heapSize个位置。重复这个步骤,就是在进行排序。
public int [] heapSort(int[] nums) {
int heapSize = nums.length;
// 先简单构造一份大根堆
buildMaxHeap(nums, heapSize);
for (int i = nums.length - 1; i >= 0; --i) {
// 每次用堆顶元素和“最后”一个数字进行交换(第一次堆顶和倒数一个数字进行交换,
// 第二次堆顶和倒数第二个数字交换,因为倒数第一个数字已经在最终位置了)
swap(nums, 0, i);
--heapSize;
maxHeapify(nums, 0, heapSize);
}
return nums;
}
完整代码
public int [] heapSort(int[] nums) {
int heapSize = nums.length;
// 先简单构造一份大根堆
buildMaxHeap(nums, heapSize);
for (int i = nums.length - 1; i >= 0; --i) {
// 每次用堆顶元素和“最后”一个数字进行交换(第一次堆顶和倒数一个数字进行交换,
// 第二次堆顶和倒数第二个数字交换,因为倒数第一个数字已经在最终位置了)
swap(nums, 0, i);
--heapSize;
maxHeapify(nums, 0, heapSize);
}
return nums;
}
// 构造大根堆
public void buildMaxHeap(int[] a, int heapSize) {
for (int i = heapSize / 2; i >= 0; --i) {
// 这里最“起码”能将最大的数字上浮至堆顶,
maxHeapify(a, i, heapSize);
}
}
// 当前index和它的左右子树进行的操作。
// (1)挑出,当前左节点left(left = 2 * i + 1)指向的数字,当前右节点right( right = 2 * i + 2)指向的数字,中较大的,
// 与largest( = index )进行交换
// (2)然后让largest( = max(left,right))指向的元素和其左右子树进行交换,重复(1),直到当前指向没有左右子树,或者左右子树都比当前指向的数字小
public void maxHeapify(int[] a, int i, int heapSize) {
int l = i * 2 + 1, r = i * 2 + 2, largest = i;
// (1)挑出,当前左节点l指向的数字,当前右节点r指向的数字,中较大的,
// 与largest进行交换
// (2)然后让largest指向的元素和heapSize指向的元素进行比较
// 进行(1),直到
if (l < heapSize && a[l] > a[largest]) {
largest = l;
}
if (r < heapSize && a[r] > a[largest]) {
largest = r;
}
if (largest != i) {
swap(a, i, largest);
maxHeapify(a, largest, heapSize);
}
}
(8)计数排序
package 十大排序;
public class CountingSort {
public int[] sort(int []A) {
// 获得最大和最小的值
int maxValue = A[0];
int minValue = A[0];
for (int i = 0; i < A.length; i++) {
maxValue = Math.max(maxValue, A[i]);
minValue = Math.min(minValue, A[i]);
}
return countingSort(A, minValue, maxValue);
}
public int getMaxValue(int []A) {
int maxNum = A[0];
for (int i = 0;i < A.length; i++) {
maxNum = Math.max(A[i], maxNum);
}
return maxNum;
}
public int []countingSort(int []A, int minValue, int maxValue) {
int bucketPosLen = maxValue + 1;
int bucketNegLen = -1 * minValue + 1;
int []bucketPos = new int[bucketPosLen];
int []bucketNeg = new int[bucketNegLen];
for (int value : A) {
if (value >= 0) {
bucketPos[value]++;
} else{
bucketNeg[-1 * value]++;
}
}
int sortIndex = 0;
// 开始排序从0至最大的数字进行排序,如果有那个数字,则数字出现的次数减少1
for (int i = minValue; i < 0; i++) {
while (bucketNeg[-1 * i] > 0) {
A[sortIndex++] = i;
bucketNeg[-1 * i]--;
}
}
for (int i = 0; i < bucketPosLen; i++) {
while (bucketPos[i] > 0) {
A[sortIndex++] = i;
bucketPos[i]--;
}
}
return A;
}
public static void main(String[] args) {
int []A = {-1, 3 , 1, 3, 1, 9 , 3 , -100, 8288};
A = new CountingSort().sort(A);
for (int i = 0; i < A.length; i++) {
System.out.print(A[i] + " ");
}
}
}
(9)桶排序
(10)基数排序
package 十大排序;
import java.util.Arrays;
public class RadixSort {
public void sort(int []A) {
// 获得最大数字的位数
int maxDigit = getNumLength(getMaxDigit(A));
radixSort(A, maxDigit);
}
// 获取最高位数
public int getMaxDigit(int []A) {
int maxValue = A[0];
for (int i = 1; i < A.length; i++) {
maxValue = maxValue > A[i] ? maxValue : A[i];
}
return maxValue;
}
// 获取数字的长度
public int getNumLength(long num) {
int sum = 0;
while (num > 0) {
num /= 10;
sum++;
}
// 判断sum为零的情况
return sum == 0 ? 1 : sum;
}
public void radixSort(int []A, int maxDigit) {
// 取模用的
int mod = 10;
// 结合mod,用来取得对应位置上的数字
int dev = 1;
for (int i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
// 考虑为负数的情况,这里拓展为一倍队列数,其中【0-9】对应负数,
// 【10-19】对应为正数(bucket + 10)
int [][] counter = new int[mod * 2][0];
for (int j = 0; j < A.length; j++) {
// 这里采用的是最低位,有的方法可能采取最高位(从高至低,从低至高)
int bucket = ((A[j] % mod) / dev) + mod;
// 根据当前数字上的对应的位上的数字,将数字放入相应的桶中
// 比如34,现在计算到了第一位,于是将34放到13对应的桶中,下一次计算到了第二位,于是将34放到14对应的桶中
counter[bucket] = arrayAppend(counter[bucket], A[j]);
// 在当前行数组后面添加元素
// 可能有的数字特立独行,特别长,但是大部分数字都很短,但是这样并不影响,想想为什么?
// 因为那些短的数字已经排好了序,再取出来也是哪个顺序,所以并不会有所影响
}
int pos = 0;
// 查看桶的变化
for (int j = 0; j < counter.length; j++) {
System.out.print(j + " ");
for (int k = 0; k < counter[j].length; k++) {
System.out.print(counter[j][k] + " ");
}
System.out.println();
}
// 从桶将数据取出来,然后放到原数组中,
for (int []bucket : counter) {
for (int value : bucket) {
A[pos++] = value;
}
}
}
}
/**
* 自动扩容,并保存数据
*/
public int[] arrayAppend(int []A, int value) {
A = Arrays.copyOf(A, A.length + 1);
A[A.length - 1] = value;
return A;
}
public static void main(String[] args) {
int []A = {1, 2123, 37, 45};
new RadixSort().sort(A);
for (int i = 0; i < A.length; i ++) {
System.out.println(A[i]);
}
}
}