可能有一年没有刷题了吧,代码能力已经白痴到不能再白痴。定个小目标,一天刷上一题。
1. 两数之和(leetcode界的abandon)
题目要求:
给定一个整数数组nums和一个目标值target,请你在该数组中找出和为目标值的那两个整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素不能使用两遍。
思路一:
遍历整个数组,计算每个元素和目标值的差,然后在这个元素之后的元素中找到差所在的位置。时间复杂度(O(n^2)),空间复杂度(O(1))。
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
n = len(nums)
for i in range(n):
diff = target - nums[i]
if diff in nums[i:]:
j = nums.index(diff)
if i != j:
return [i, j]
思路二:
建立一个哈希表,以空间换时间。每次迭代计算当前元素与目标值的差,判断差是否在哈希表中,如果没有匹配就将当前的元素加入哈希表中,如num[i]:i。时间复杂度(O(n)),空间复杂度(O(n))。
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
hashmap = {}
for index, num in enumerate(nums):
diff = target - num
if diff in hashmap:
return [hashmap[diff], index]
hashmap[num] = index
思路一耗时大概1000ms,思路二耗时大概40ms。可见速度快了很多。
2. 两数相加
题目要求:
给出两个非空的链表用来表示两个非负的整数。其中,它们各自的位数是按照逆序的方式存储的,并且它们的每个节点只能存储一位数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字0之外,这两个数都不会以0开头。
思路:
既然是逆序存储就好办了,直接按顺序加就行了,有进位的话在最后再加上一个结点就好。时间复杂度(O(max(m, n))),空间复杂度(O(1))。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def addTwoNumbers(self, l1: ListNode, l2: ListNode) -> ListNode:
carry = 0
r = ListNode(0)
result = r
while l1 or l2:
a, b = l1.val if l1 else 0, l2.val if l2 else 0
c = a + b + carry
carry = c // 10
c = c % 10
result.next = ListNode(c)
result = result.next
if l1: l1 = l1.next
if l2: l2 = l2.next
if carry:
result.next = ListNode(carry)
return r.next
23. 合并K个排序链表
题目要求:
合并k个排序链表,返回合并后的排序链表。请分析和描述算法的复杂度。
思路:
数据结构学过归并两个链表,那么只要把若干个链表两两归并即可。假设链表的平均长度为n,一共有k个链表,每次归并的时间复杂度为(O(n)),一共需要
次归并,于是总时间复杂度为(O(kn log k)),空间复杂度为(O(1))
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def mergeKLists(self, lists: List[ListNode]) -> ListNode:
n = len(lists)
if n == 0:
return None
def merge2Lists(L1, L2):
ptr = ListNode(0)
head = ptr # 头结点
while L1 and L2:
if L1.val < L2.val:
ptr.next = L1
L1 = L1.next
else:
ptr.next = L2
L2 = L2.next
ptr = ptr.next
ptr.next = L1 if L1 else L2
return head.next
step = 1
while step < n:
for i in range(0, n - step, step * 2):
# n - step可以保证两两相归并时 i + step不超出索引范围
lists[i] = merge2Lists(lists[i], lists[i + step])
step *= 2
return lists[0]
33. 搜索旋转排序数组
题目要求:
假设按照升序排序的数组在预先未知的某个点上进行了旋转。例如,数组[0,1,2,4,5,6,7]可能变为[4,5,6,7,0,1,2]。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回-1。你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是(O(log n))级别。
思路:
题目中要求算法时间复杂度必须是(O(log n)),且数组是由有序数组旋转而来,显然得用二分搜索。
- 如果
mid处的元素大于left处的元素,说明mid左侧的数组是有序的;如果nums[left] <= target < nums[mid],那么就在左侧继续查找,否则就到右侧查找。 - 如果
mid处的元素小于left处的元素,说明mid右侧的数组是有序的;如果nums[mid] <= target < nums[right],那么就在右侧继续查找,否则就到左侧查找。
class Solution:
def search(self, nums: List[int], target: int) -> int:
n = len(nums)
left, right = 0, n - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
if nums[left] <= nums[mid]:
if nums[left] <= target < nums[mid]:
right = mid - 1
else:
left = mid + 1
else:
if nums[mid] < target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1
41. 缺失的第一个正数
题目要求:
给你一个未排序的整数数组,请你找出其中没有出现的最小的正整数。
提示:
你的算法的时间复杂度应为(O(n)),并且只能使用常数级别的额外空间。
思路:
第一想法是建立一个哈希表,把数组中的元素放到哈希表中,再看哪个正整数少了。但是题目要求只能用(O(1))的空间。那咋办嘛?那就用数组的索引做哈希表,遍历数组,如果数组中的元素在1 ~ n范围内,就放到数组中相应的位置上。时间复杂度(O(n)),空间复杂度(O(1))。
class Solution:
def firstMissingPositive(self, nums: List[int]) -> int:
if(not nums):
return 1
n = len(nums)
# 不用额外建立哈希表,利用本身的索引即可
for i in range(n):
while(1 <= nums[i] <= n and nums[i] != nums[nums[i] - 1]):
# 注意:nums[nums[i] - 1]和nums[i]的位置不能换,否则会出错
nums[nums[i] - 1], nums[i] = nums[i], nums[nums[i] - 1]
for i in range(n):
if(nums[i] != i+1):
return i + 1
return n + 1
46. 全排列
题目要求:
给定一个没有重复数字的序列,返回其所有可能的全排列。
思路:
之前看过一个B站的视频,讲的就是这一题。
- 首先遍历这个数组,要让数组中的每一个元素都当一次第一;
- 接着让这个元素之后的子数组,同样地让每一个元素当一次第一(递归实现);
- 最后要回溯,即让第一回到它原来的位置,否则会造成结果不完整且重复。
class Solution:
def permute(self, nums: List[int]) -> List[List[int]]:
def backTrac(i, j):
if i == n:
res.append(nums[:])
else:
for index in range(i, n):
nums[i], nums[index] = nums[index], nums[i]
backTrac(i + 1, n)
nums[i], nums[index] = nums[index], nums[i]
n = len(nums)
res = []
backTrac(0, n)
return res
48. 旋转图像
题目要求:
给定一个n×n的二维矩阵表示一个图像。将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
思路:
观察发现,将矩阵旋转90度相当于先将矩阵转置,再把每一行的元素逆序。时间复杂度(O(n^2)),空间复杂度(O(1))。
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
"""
Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
# 先将矩阵转置
for i in range(n):
for j in range(i, n):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
for i in range(n):
for j in range(n//2):
matrix[i][j], matrix[i][n - j - 1] = matrix[i][n - j - 1], matrix[i][j]
看了官方解答中的后两个方法,有点复杂,还是这么做比较好理解。
49. 字母异位词分组
题目要求:
给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。
说明:
- 所有输入均为小写字母。
- 不考虑答案输出的顺序。
思路:
将字符串排序,然后扔到字典里。时间复杂度(O(nlog n)),空间复杂度(O(n))。
class Solution:
def groupAnagrams(self, strs: List[str]) -> List[List[str]]:
hashmap = {}
ans = []
for s in strs:
key = ''.join(sorted(s))
if key not in hashmap:
hashmap[key] = [s]
else:
hashmap[key].append(s)
for val in hashmap.values():
ans.append(val)
return ans
66. 加一
题目要求:
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。
最高位数字存放在数组的首位,数组中每个元素只存储单个数字。
你可以假设除了整数 0 之外,这个整数不会以零开头。
思路:
只有特殊的数字如999才会使得最终的数组比原数组长一位,因此只要倒序遍历,如果没有进位就返回,如果都遍历完了还有进位,就返回1000。时间复杂度(O(n)),空间复杂度(O(n))。
class Solution:
def plusOne(self, digits: List[int]) -> List[int]:
n = len(digits)
for i in range(n - 1, -1, -1):
digits[i] += 1
carry = digits[i]//10
digits[i] = digits[i] % 10
if not carry:
return digits
return [1] + [0] * n
91. 解码方法
题目要求:
一条包含字母A-Z的消息通过以下方式进行了编码:
'A' -> 1
'B' -> 2
...
'Z' -> 26
给定一个只包含数字的非空字符串,请计算解码方法的总数。
思路:
当前字符串的解码方法数可以从它子串的解码数推导出来,可以用动态规划的方法。
- 显然空字符串和首位是
0的字符串是不能解码的; - 当前位置是
0时,当且仅当前一位是1或2才能解码; - 当前位置非零时,若前一位是
1或前一位是2且当前位是0~6时,那么当前位置既可以单独解码也可以与前一位向结合解码。
时间复杂度(O(n)),空间复杂度(O(n))。
class Solution:
def numDecodings(self, s: str) -> int:
n = len(s)
# 判断字符串是否为空或首位是否为0,若成立则不能编码
if(not s or s[0] == '0'):
return 0
dp = [0] * (n+1)
dp[0] = 1
dp[1] = 1
for i in range(1, n):
# 当前位置是0时,只能与前一个数结合才能解码
if(s[i] == '0'):
if(s[i - 1] == '1' or s[i - 1] == '2'):
dp[i + 1] = dp[i - 1]
else:
return 0
# 当前位置不是0时,分两种情况
else:
# 满足以下条件,则既可以与前一个数字结合,也可以单独解码
if(s[i-1] == '1' or (s[i - 1] == '2' and '1' <= s[i] <= '6')):
dp[i + 1] = dp[i] + dp[i - 1]
# 否则只能单独解码
else:
dp[i + 1] = dp[i]
return dp[-1]
118. 杨辉三角
题目要求:
给定一个非负整数numRows,生成杨辉三角的前numRows行。在杨辉三角中,每个数是它左上方和右上方的数的和。
思路一:
题目中已经写得很清楚了,每个数是它左上方和右上方的数的和,按这个规则计算就行了。要注意特判,因为前两行无法套用这个规则。时间复杂度(O(n^2)),空间复杂度(O(1))。
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
if numRows == 0:
return []
elif numRows == 1:
return [[1]]
tri = [[1], [1, 1]]
for i in range(2, numRows):
tri.append([1] + [tri[i - 1][j] + tri[i - 1][j + 1] for j in range(0, i - 1)] + [1])
return tri
思路二:
在评论区看到一位大佬的思路,将杨辉三角的计算看作是错位相加:
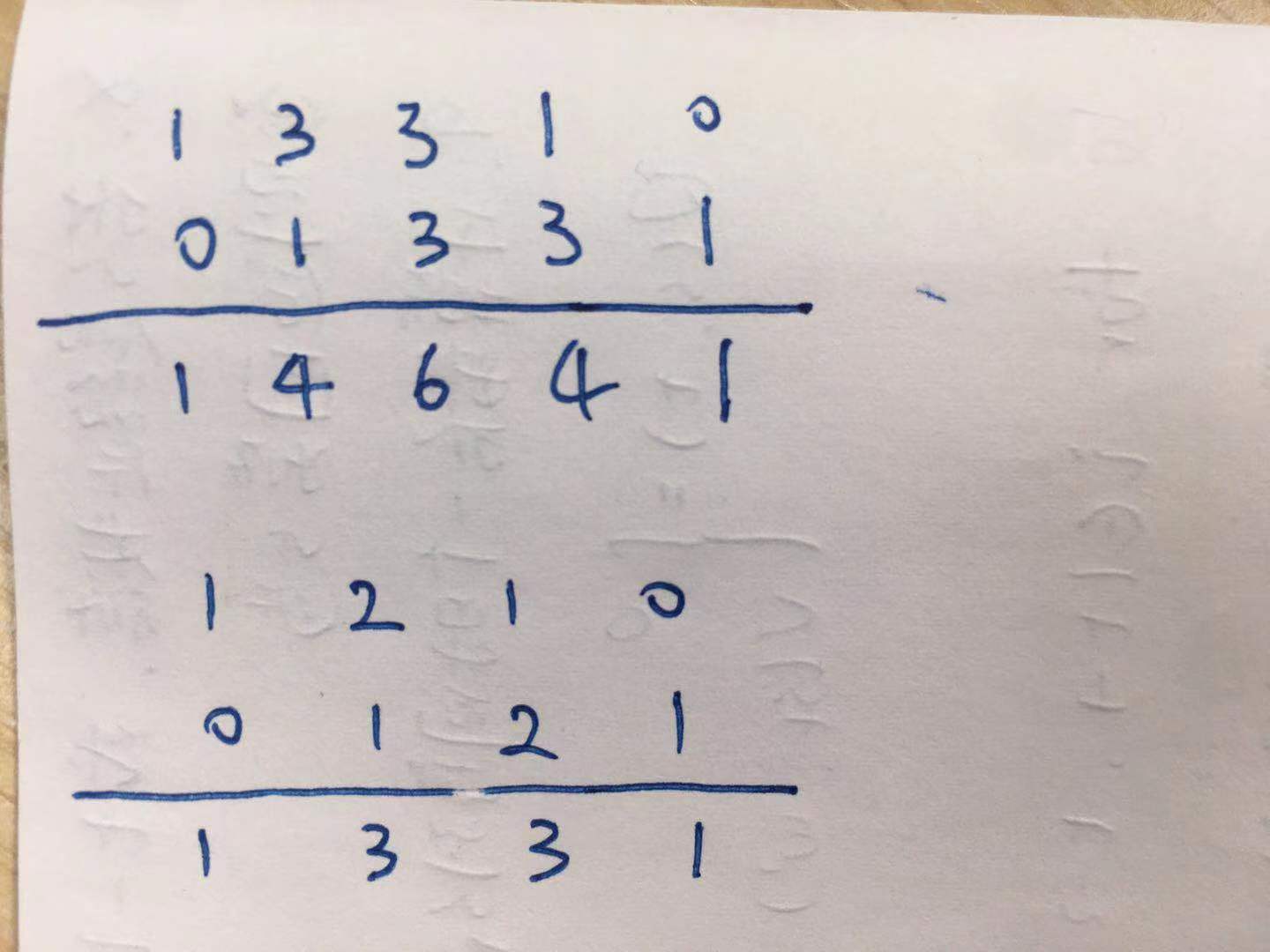
class Solution:
def generate(self, numRows: int) -> List[List[int]]:
if numRows == 0:
return []
tri = [[1]]
while len(tri) < numRows:
newRow = [a + b for a, b in zip([0] + tri[-1], tri[-1] + [0])]
tri.append(newRow)
return tri
121. 买卖股票的最佳时机
题目要求:
给定一个数组,它的第i个元素是一支给定股票第i天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票一次),设计一个算法来计算你所能获取的最大利润。注意:你不能在买入股票前卖出股票。
思路一:
暴力解法,即用双重循环,外循环遍历数组的每一个元素,内循环遍历每个元素之前的元素,找到最大的利润。时间复杂度(O(n^2)),空间复杂度(O(1))。
思路二:
将每次找到的最低价格记录下来,就不需要再每次去前面的元素中找了。时间复杂度(O(n)),空间复杂度(O(1))。
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if len(prices) < 2:
return 0
max_pr = 0 # 最大收益
min_pr = prices[0] #最低价格
for x in prices:
max_pr = max(x - min_pr, max_pr)
min_pr = min(x, min_pr)
return max_pr
151. 翻转字符串里的单词
题目要求:
给定一个字符串,逐个翻转字符串中的每个单词。
说明:
- 无空格字符构成一个单词。
- 输入字符串可以在前面或者后面包含多余的空格,但是反转后的字符不能包括。
- 如果两个单词间有多余的空格,将反转后单词间的空格减少到只含一个。
思路:
python可以直接split然后逆序输出就解决了。自己实现的话,先要把开头和结尾的多余空格去掉,再用两个指针寻找字符串中单词的位置,找到后丢到数组中。时间复杂度(O(n)),空间复杂度(O(n))。
class Solution:
def reverseWords(self, s: str) -> str:
ans = []
n = len(s)
if n == 0:
return ''
lo, hi = 0, n - 1
# 去掉首尾的空格,字符串可能全是空格,因此while循环要判断lo<=hi
while lo <= hi and s[lo] == ' ':
lo += 1
while lo <= hi and s[hi] == ' ':
hi -= 1
# left和right指向单词的开头和结尾
left = right = hi
while left >= lo:
while left >= lo and s[left] != ' ':
left -= 1
ans.append(s[left + 1: right + 1])
while s[left] == ' ':
left -= 1
right = left
return ' '.join(ans)
182. 查找重复的电子邮箱
题目要求:
编写一个SQL查询,查找Person表中所有重复的电子邮箱。(怎么还有MySQL,头大)
select Email from Person
group by Email
having count(Email) > 1;
注意group by 后需要用having。
215. 数组中的第K个最大元素
题目要求:
在未排序的数组中找到第k个最大的元素。请注意,你需要找的是数组排序后的第k个最大的元素,而不是第k个不同的元素。
思路:
这题可以用内置的排序函数耍赖皮,但是这样就没啥意思了,就顺便复习一下堆排序吧。找第k大的元素,换言之,找前k大中最小的元素,这样就自然而然地想到了堆排序。把数组的前k个位置弄成一个小顶堆,然后继续遍历之后的元素,只要当前元素小于第一个元素,将他们交换,然后调整堆。最终数组的第一个元素就是我们要找的第k大的元素。时间复杂度(O(nlog{k})),空间复杂度(O(1))。
class Solution:
def findKthLargest(self, nums: List[int], k: int) -> int:
def heapify(lo):
min_ = i = lo
j = 2 * i + 1
while j < k:
if j + 1 < k and nums[j + 1] < nums[j]:
j += 1
if nums[j] < nums[min_]:
nums[min_], nums[j] = nums[j], nums[min_]
i = j
j = 2 * i + 1
else:
break
min_ = i
n = len(nums)
for i in range(k // 2 - 1, -1, -1):
heapify(i)
for i in range(k, n):
if nums[i] > nums[0]:
nums[i], nums[0] = nums[0], nums[i]
heapify(0)
return nums[0]
237. 删除链表中的节点
题目要求:
请编写一个函数,使其可以删除某个链表中给定的(非末尾)节点,你将只被给定要求被删除的节点。现有一个链表 --head = [4,5,1,9],它可以表示为:

说明:
- 链表至少包含两个节点。
- 链表中所有节点的值都是唯一的。
- 给定的节点为非末尾节点并且一定是链表中的一个有效节点。
- 不要从你的函数中返回任何结果。
思路:
刚看到这题可给爷整懵逼了,只给定结点没有给链表,那我要怎么找到这个结点的前一个结点呢?这大概就是思维定势吧。题目的说明中提到给定的结点是非末尾结点,那么其实只要把后一个结点的值赋值给当前结点,再把next指向下下个结点就行了。时间复杂度(O(1)),空间复杂度(O(1))。
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def deleteNode(self, node):
"""
:type node: ListNode
:rtype: void Do not return anything, modify node in-place instead.
"""
node.val, node.next = node.next.val, node.next.next
278. 第一个错误的版本
题目要求:
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有n个版本[1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用bool isBadVersion(version)接口来判断版本号 version是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
思路:
题目提到尽量减少API的调用,也就是减少查找次数。而版本的错误与否其实是”有序的“,都是形如[false, ..., false, true, ..., true],因此用二分查找就行了。
# The isBadVersion API is already defined for you.
# @param version, an integer
# @return a bool
# def isBadVersion(version):
class Solution:
def firstBadVersion(self, n):
"""
:type n: int
:rtype: int
"""
left, right = 1, n
while(left < right):
mid = (left + right)//2
if isBadVersion(mid):
right = mid
else:
left = mid + 1
return left
283. 移动零
题目要求:
给定一个数组nums,编写一个函数将所有0移动到数组的末尾,同时保持非零元素的相对顺序。
思路:
利用两个指针,指针left指向数组中的第一个0,指针right指向数组中0之后的第一个非零元素,交换位置即可。时间复杂度(O(n)),空间复杂度(O(1))。
class Solution:
def moveZeroes(self, nums: List[int]) -> None:
"""
Do not return anything, modify nums in-place instead.
"""
len_arr = len(nums)
left = right = 0
while right < len_arr:
if nums[right] != 0:
nums[left], nums[right] = nums[right], nums[left]
left += 1
right += 1
else:
right += 1
289. 生命游戏
题目要求:
生命游戏,是英国数学家约翰·何顿·康威在1970年发明的细胞自动机。
给定一个包含m × n个格子的面板,每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态:1即为活细胞(live),或0即为死细胞(dead)。每个细胞与其八个相邻位置(水平,垂直,对角线)的细胞都遵循以下四条生存定律:
- 如果活细胞周围八个位置的活细胞数少于两个,则该位置活细胞死亡;
- 如果活细胞周围八个位置有两个或三个活细胞,则该位置活细胞仍然存活;
- 如果活细胞周围八个位置有超过三个活细胞,则该位置活细胞死亡;
- 如果死细胞周围正好有三个活细胞,则该位置死细胞复活;
根据当前状态,写一个函数来计算面板上所有细胞的下一个(一次更新后的)状态。下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的,其中细胞的出生和死亡是同时发生的。
思路一:
根据题意,如果没有做到同时更新,就可能会有多种答案。因此创建一个辅助数组用来存当前的细胞状态,原数组用来更新细胞的状态。这里遇到了一个深复制和浅复制的坑,二维数组用.copy()仍然是浅复制,还是乖乖用列表生成式吧。
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
m, n = len(board), len(board[0])
board_copy = [[board[row][col] for col in range(n)] for row in range(m)]
goto = [[0, 1], [1, 0], [0, -1], [-1, 0], [1, 1], [1, -1], [-1, 1], [-1, -1]]
for i in range(m):
for j in range(n):
live_cnt = 0
for k in goto:
r, c = i + k[0], j + k[1]
if (r >= 0 and r < m) and (c >= 0 and c < n) and (board_copy[r][c] == 1):
live_cnt += 1
if board_copy[i][j] == 1 and (live_cnt < 2 or live_cnt > 3):
board[i][j] = 0
if board_copy[i][j] == 0 and live_cnt == 3:
board[i][j] = 1
思路二:
改变状态的编码形式,如果原来是活的后来死了,记为-1;如果原来是死的后来活了,记为2;如果原来是活的后来还是活的,仍记为1。这么一来就不需要辅助数组了。
class Solution:
def gameOfLife(self, board: List[List[int]]) -> None:
"""
Do not return anything, modify board in-place instead.
"""
m, n = len(board), len(board[0])
goto = [[0, 1], [1, 0], [0, -1], [-1, 0], [1, 1], [1, -1], [-1, 1], [-1, -1]]
for i in range(m):
for j in range(n):
live_cnt = 0
for k in goto:
r, c = i + k[0], j + k[1]
if (0 <= r < m) and (0 <= c < n) and abs(board[r][c]) == 1:
live_cnt += 1
if board[i][j] == 1 and (live_cnt < 2 or live_cnt > 3):
board[i][j] = -1
elif board[i][j] == 0 and live_cnt == 3:
board[i][j] = 2
for i in range(m):
for j in range(n):
if board[i][j] <= 0:
board[i][j] = 0
else:
board[i][j] = 1
在评论区还发现一个大佬的思路:一个细胞受周围八个细胞的影响,那么同理,一个细胞也可以影响它周围的八个细胞。于是可以遍历整个二维数组,如果当前的细胞是活的,那么它周围的八个位置都加上10,这样最后得到的结果十位是周围的活细胞数量,个位是上一个时间该细胞的状态。再遍历一次数组就能得到更新后的状态。
345. 反转字符串中的元音字母
题目要求:
编写一个函数,以字符串作为输入,反转该字符串中的元音字母。
思路:
利用两个指针,从字符串的两边出发,找到元音字母后互换。时间复杂度(O(n)),空间复杂度(O(1))。第一次写出的代码是下面这样的:
class Solution:
def reverseVowels(self, s: str) -> str:
str_list = list(s)
len_ = len(str_list)
left, right = 0, len_ - 1
str2 = 'aeiouAEIOU'
while left < right:
while str_list[left] not in str2 and left < right:
left += 1
while str_list[right] not in str2 and left < right:
right -= 1
if left < right:
str_list[left], str_list[right] = str_list[right], str_list[left]
left += 1
right -= 1
return ''.join(str_list)
这种一次移动几次指针的操作看起来更快,但实际上需要多几次left < right的判断,还是亏了。于是看了看评论区,发现都是一次移动一下指针,这么一来反而不需要那么多次判断,而且时间复杂度是不会变的。
class Solution:
def reverseVowels(self, s: str) -> str:
str_list = list(s)
len_ = len(str_list)
# 字符串不能更改,要转为数组
left, right = 0, len_ - 1
str2 = 'aeiouAEIOU'
while left < right:
if str_list[left] in str2 and str_list[right] in str2:
str_list[left], str_list[right] = str_list[right], str_list[left]
left += 1
right -= 1
if str_list[left] not in str2:
left += 1
if str_list[right] not in str2:
right -= 1
return ''.join(str_list)
357. 计算各个位数不同的数字个数
题目要求:
给定一个非负整数n,计算各位数字都不同的数字x的个数,其中(0 le x < 10^{n}) 。
思路:
首先对于n位数来说,第一位是不能取0的,可以有9种选择,下一位有9种选择(包括0),再下一位有8种选择...以此类推。题目要求的是(0 le x < 10^{n})中各位都不同的数字,显然n位数的个数加上n - 1位数的个数就是所求的结果。还有一个需要注意的地方是当n大于10时,它的个数就不变了,因为一共就10个数字。这是典型的动态规划问题。时间复杂度(O(n)),空间复杂度(O(1))。
class Solution:
def countNumbersWithUniqueDigits(self, n: int) -> int:
if n==0:
return 1
cnt, cnt_pre = 10, 9
for i in range(2, min(11, n + 1)):
cnt_pre *= 10 - i + 1
cnt += cnt_pre
return cnt
404. 左叶子之和
题目要求:
计算给定二叉树的所有左叶子之和。
思路:
在遍历的同时判断是否是左叶子即可。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def sumOfLeftLeaves(self, root: TreeNode) -> int:
if not root:
return 0
if root and root.left and not root.left.left and not root.left.right:
return root.left.val + self.sumOfLeftLeaves(root.right)
return self.sumOfLeftLeaves(root.left) + self.sumOfLeftLeaves(root.right)
412. Fizz Buzz
题目要求:
写一个程序,输出从 1 到 n 数字的字符串表示。
- 如果
n是3的倍数,输出“Fizz”; - 如果
n是5的倍数,输出“Buzz”; - 如果
n同时是3和5的倍数,输出 “FizzBuzz”。
思路一:
直接遍历更改相应的元素就行了。时间复杂度(O(n)),空间复杂度(O(1))。
class Solution:
def fizzBuzz(self, n: int) -> List[str]:
res = [str(i) for i in range(1, n + 1)]
for index in range(n):
if (index + 1) % 15 == 0:
res[index] = "FizzBuzz"
elif (index + 1) % 3 == 0:
res[index] = "Fizz"
elif (index + 1) % 5 == 0:
res[index] = "Buzz"
return res
思路二:
官方解答更具有一般性,如果能被三整除,就加上Fizz;如果能被五整除,就加上Buzz。时间复杂度(O(n)),空间复杂度(O(1))。
class Solution:
def fizzBuzz(self, n: int) -> List[str]:
res = []
for i in range(n):
ans = ""
if (i + 1) % 3 == 0:
ans += "Fizz"
if (i + 1) % 5 == 0:
ans += "Buzz"
if not ans:
ans = str(i + 1)
res.append(ans)
return res
595. 大的国家
题目要求:
这里有张World 表
| name | continent | area | population | gdp |
|---|---|---|---|---|
| Afghanistan | Asia | 652230 | 25500100 | 20343000 |
| Albania | Europe | 28748 | 2831741 | 12960000 |
| Algeria | Africa | 2381741 | 37100000 | 188681000 |
| Andorra | Europe | 468 | 78115 | 3712000 |
| Angola | Africa | 1246700 | 20609294 | 100990000 |
如果一个国家的面积超过300万平方公里,或者人口超过2500万,那么这个国家就是大国家。
编写一个SQL查询,输出表中所有大国家的名称、人口和面积。
例如,根据上表,我们应该输出:
| name | continent | area | population | gdp |
|---|---|---|---|---|
| Afghanistan | Asia | 652230 | 25500100 | 20343000 |
| Algeria | Africa | 2381741 | 37100000 | 188681000 |
# Write your MySQL query statement below
select name, population, area from World
where area > 3000000
or
population > 25000000;
700. 二叉搜索树中的搜索
题目要求:
给定二叉搜索树(BST)的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在,则返回 NULL。
思路:
这是一个二叉搜索树,左子树中结点的值总是小于根结点,右子树中结点的值总是大于根结点。那么左右横跳就行了。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def searchBST(self, root: TreeNode, val: int) -> TreeNode:
if not root or root.val == val:
return root
if val > root.val:
return self.searchBST(root.right, val)
else:
return self.searchBST(root.left, val)
881. 救生艇
题目要求:
第i个人的体重为people[i],每艘船可以承载的最大重量为limit。每艘船最多可同时载两人,但条件是这些人的重量之和最多为limit。返回载到每一个人所需的最小船数。(保证每个人都能被船载)。
思路:
一开始想的是先排序,然后按顺序两两配对,事实证明这样会造成大量的空间浪费,最后大体重的人不得不一个人乘一艘船。我真是太菜了。正确的思路应该是将最重的人与最轻的人配对,这样才能求出最优解。时间复杂度(O(nlog n)),空间复杂度(O(1))。
class Solution:
def numRescueBoats(self, people: List[int], limit: int) -> int:
people.sort()
len_arr = len(people)
cnt = 0
left, right = 0, len_arr - 1
while left <= right:
cnt += 1
# 如果当前最胖的和最瘦的可以配对,那么他们就乘坐同一艘船
if people[left] + people[right] <= limit:
left += 1
right -= 1 # 为下一个胖子寻找配对
return cnt
969. 煎饼排序
题目要求:
给定数组A,我们可以对其进行煎饼翻转:我们选择一些正整数k<= A.length,然后反转A的前k个元素的顺序。我们要执行零次或多次煎饼翻转(按顺序一次接一次地进行)以完成对数组A的排序。
返回能使A排序的煎饼翻转操作所对应的k值序列。任何将数组排序且翻转次数在10 * A.length范围内的有效答案都将被判断为正确。
提示:
1 <= A.length <= 100A[i]是[1, 2, ..., A.length]的排列
思路:
可以按照这样的顺序进行排序:首先找到最大的元素,将其翻转到第一位;再翻转整个数组,它就到达该到的位置。
class Solution:
def pancakeSort(self, A: List[int]) -> List[int]:
n = len(A)
ans = []
for i in range(n - 1, -1, -1):
max_ = i
for j in range(0, i + 1):
if A[j] == (i + 1):
max_ = j
if max_ != i:
A[:max_ + 1] = A[:max_ + 1][::-1]
A[:i + 1] = A[:i + 1][::-1]
ans.extend([max_ + 1, i + 1])
return ans
1095. 山脉数组中查找目标值
题目要求:
给你一个 山脉数组mountainArr,请你返回能够使得mountainArr.get(index)等于target最小的下标index值。如果不存在这样的下标index,就请返回-1。
何为山脉数组?如果数组A是一个山脉数组的话,那它满足如下条件:
首先,A.length >= 3
其次,在0 < i < A.length - 1条件下,存在i使得:
A[0] < A[1] < ... A[i-1] < A[i]A[i] > A[i+1] > ... > A[A.length - 1]
你将不能直接访问该山脉数组,必须通过MountainArray接口来获取数据:
MountainArray.get(k)- 会返回数组中索引为k的元素(下标从 0 开始)MountainArray.length()- 会返回该数组的长度
注意:
对MountainArray.get发起超过100次调用的提交将被视为错误答案。
提示:
3 <= mountain_arr.length() <= 100000 <= target <= 10^90 <= mountain_arr.get(index) <= 10^9
思路:
题中要求不能超过100次调用,数组长度不超过10000,疯狂明示要用二分查找。而山脉数组以山顶为界限,两边都是有序的,因此要用二分查找关键在于怎么找到山顶。首先将数组二分:- 如果mid处的元素比它右边的元素小,那它一定不是山顶,left = mid + 1;
- 否则
mid有可能是山顶,right = mid
循环结束后right就是山顶。找到山顶后就可以在两边有序的数组中用二分查找搜索目标元素。
# """
# This is MountainArray's API interface.
# You should not implement it, or speculate about its implementation
# """
#class MountainArray:
# def get(self, index: int) -> int:
# def length(self) -> int:
class Solution:
def findInMountainArray(self, target: int, mountain_arr: 'MountainArray') -> int:
n = mountain_arr.length()
left, right = 0, n - 1
# 循环结束后right就是山顶
while left < right:
top = (left + right) // 2
if mountain_arr.get(top) > mountain_arr.get(top + 1):
right = top
else:
left = top + 1
left, top = 0, right
while left <= right:
mid = (left + right) // 2
val = mountain_arr.get(mid)
if val == target:
return mid
elif val > target:
right = mid - 1
else:
left = mid + 1
left, right = top + 1, n - 1
while left <= right:
mid = (left + right) // 2
val = mountain_arr.get(mid)
if val == target:
return mid
elif val < target:
right = mid - 1
else:
left = mid + 1
return -1
1401. 圆和矩形是否有重叠
题目要求:
给你一个以(radius, x_center, y_center)表示的圆和一个与坐标轴平行的矩形(x1, y1, x2, y2),其中(x1, y1)是矩形左下角的坐标,(x2, y2)是右上角的坐标。
如果圆和矩形有重叠的部分,请你返回True ,否则返回 False。
换句话说,请你检测是否存在点(xi, yi),它既在圆上也在矩形上(两者都包括点落在边界上的情况)。
思路:
以矩形的中心为原点建立直角坐标系,将圆映射到第一象限,显然对结果没有影响,再计算圆心与矩形之间的距离。参考了知乎的一个回答。
class Solution:
def checkOverlap(self, radius: int, x_center: int, y_center: int, x1: int, y1: int, x2: int, y2: int) -> bool:
rcenter_x, rcenter_y = (x1 + x2)/2, (y1 + y2)/2
v_x, v_y = abs(x_center - rcenter_x), abs(y_center - rcenter_y)
u_x, u_y = max(v_x - (x2 - rcenter_x), 0), max(v_y - (y2 - rcenter_y), 0)
return (u_x ** 2 + u_y ** 2) <= radius ** 2
1404. 将二进制表示减到 1 的步骤数
题目要求:
给你一个以二进制形式表示的数字s。请你返回按下述规则将其减少到1所需要的步骤数:
- 如果当前数字为偶数,则将其除以 2 。
- 如果当前数字为奇数,则将其加上 1 。
题目保证你总是可以按上述规则将测试用例变为1。
思路一:
用python耍个赖皮,直接将s转化为十进制的整型,这在python是允许的,其他语言可能会溢出。
class Solution:
def numSteps(self, s: str) -> int:
cnt = 0
s = int(s, 2)
while s != 1:
if s%2 == 0:
s = s//2
else:
s = s + 1
cnt += 1
return cnt
思路二:
从后往前遍历字符串,分为两种情况:
- 当没有进位时,即之前都是偶数。如果当前位置是
0,只需要一个步骤(除以2)就可以去掉这一位;如果当前位置是1,则需要两个步骤(加1再除以2,这时候就有了进位)才能去掉这一位。 - 当有进位时,即之前有过奇数。如果当前位置是
0,由于有进位,那么这一位实际上会变成1,则需要两个步骤才能去掉这一位;如果当前位置是1,进位将其变成0,则只需要一步就能去掉这一位。
class Solution:
def numSteps(self, s: str) -> int:
n, cnt = len(s), 0
carry = False
for i in range(n - 1, -1, -1):
if s[i] == '0':
if carry:
cnt += 2
else:
cnt += 1
else:
if carry:
cnt += 1
else:
# 需要考虑特殊情况(10):
# 如果已经遍历到第一个位置且之前都没有进位,那么就已经不需要再操作了
if i != 0:
cnt += 2
carry = 1
return cnt
面试题 01.07. 旋转矩阵
和48一毛一样
面试题 02.03. 删除中间节点
和237一毛一样
面试题26. 树的子结构
题目要求:
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)B是A的子结构,即A中有出现和B相同的结构和节点值。
思路:
要判断是不是子结构需要两个过程:
- 首先遍历A找到和B的根结点相同的结点X
- 判断以X为根结点的子树是否包含B
这样就需要两个递归遍历函数,一个完成第一个过程,另一个完成第二个过程。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def isSubStructure(self, A: TreeNode, B: TreeNode) -> bool:
isSub = False
if A and B:
if A.val == B.val:
isSub = self.subTrav(A, B)
if not isSub:
isSub = self.isSubStructure(A.left, B)
if not isSub:
isSub = self.isSubStructure(A.right, B)
return isSub
def subTrav(self, A, B):
if not B or not A:
return True
if A.val != B.val:
return False
return self.subTrav(A.left, B.left) and self.subTrav(A.right, B.right)
面试题61. 扑克牌中的顺子
题目要求:
从扑克牌中随机抽5张牌,判断是不是一个顺子,即这5张牌是不是连续的。2 ~ 10为数字本身,A为1,J为11,Q为12,K为13,而大、小王为0,可以看成任意数字。A不能视为14。
限制:
- 数组长度为
5 - 数组的数取值为
[0, 13]
思路:
看了半天才看懂题目,原来不是斗地主的顺子啊。
- 大小王相当于赖子,可以充当任何数;
A不能视为14,因此[10, 11, 12, 13, 1]不是顺子。
那么判断是不是顺子就要判断最大元素和最小元素之间的差要小于5,且不能有重复的元素。用一个辅助数组cnt来判断有没有重复,一旦重复就返回False。
class Solution:
def isStraight(self, nums: List[int]) -> bool:
cnt = [0] * 14
min_, max_ = 14, -1
for x in nums:
if not x:
continue
elif not cnt[x]:
cnt[x] = 1
min_ = min(min_, x)
max_ = max(max_, x)
else:
return False
return max_ - min_ < 5
LCP 02. 分式化简deep♂dark♂fraction
题目要求:
有一个同学在学习分式。他需要将一个连分数化成最简分数,你能帮助他吗?
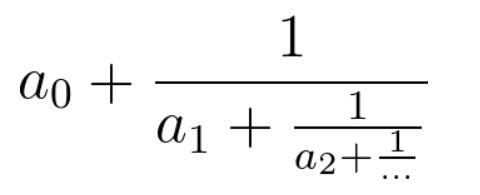
连分数是形如上图的分式。在本题中,所有系数都是大于等于0的整数。
输入的cont代表连分数的系数(cont[0]代表上图的a0,以此类推)。返回一个长度为2的数组[n, m],使得连分数的值等于n / m,且n, m最大公约数为1。
思路:
题目要求将最后的结果化简,实际上不需要约分。证明如下:
最里面的分式形式为
显然这个分式已经是最简;假设化简过程中第二步的结果为
其中(frac{c}{b})已经化简,如果(ab + c, b) != 1,则存在x, y, n,使得
于是有
则c也能被n整除,与(frac{c}{b})最简矛盾。以此类推,不需要化简。
于是代码就按照下面的等式写就好了,注意分子分母的顺序。
class Solution:
def fraction(self, cont: List[int]) -> List[int]:
len_arr = len(cont)
# 一开始第一个是分母,后一个是分子
res = [cont[-1], 1]
#迭代
for i in range(len_arr - 2, -1, -1):
# 每次迭代,解就取一次倒数;
# 至最后一次迭代,恰好又取了一次倒数,第一个是分子,后一个是分母
res[0], res[1] = cont[i]*res[0] + res[1], res[0]
return res