hdu 1007 Quoit Design, 平面最近点对

平面最近点对的经典做法就是分治。所有点先按x再按y排序，然后取中间位置的点，利用其x坐标值将点划分成左右两部分，分别求出两侧的最近点对（设其距离为δ），然后合并。参看下面的图片（来自guyulongcs的专栏，http://blog.csdn.net/guyulongcs/article/details/6841550）合并的时候需要注意，大致有两种做法，一种是把分界线两侧δ范围内的点分别加进一个数组，然后对右侧数组按y坐标值排序，之后依次为每个左侧数组中的点，在右侧数组中寻找与其y坐标值最近的6个点，并计算距离；另一种做法是，将分界线两侧δ范围内的点全部加进一个数组，然后按y坐标排序，每个点与其后面的8个点作比较，求出最近距离。理论上第一种方法更快一些,此处给出第一种 方法实现的代码：

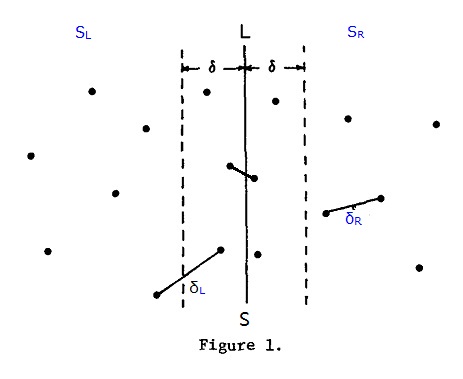
图片来源：http://images.cnblogs.com/cnblogs_com/king1302217/%E5%88%86%E6%B2%BB%E5%88%92%E5%88%86_1.jpg

方法1代码：

#include  <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
#define inf (0x3f3f3f3f)
#define N 100100
struct point{
    double x, y;
    bool operator < (const point &a) const{
        if(x == a.x) return y < a.y;
        return x < a.x;
    }
}p[N], pl[N], pr[N];

bool compy(point a, point b){
    return a.y < b.y;
}

double dist(point a, point b)
{
    double x = a.x-b.x, y = a.y-b.y;
    return x*x+y*y;
}
int fd(int l, int r, int key)
{
    while(l < r-1)
    {
        int mid = l+r>>1;
        if(pr[mid].y < key) l = mid+1;
        else r = mid;
    }
    return l;
}

double solve(int l, int r)
{
    if(l == r) return 1.0*inf;
    else if(l+1 == r) return dist(p[l], p[r]);
    int mid = l+r>>1;
    double d1 = solve(l, mid);
    double d2 = solve(mid+1, r);
    double d = min(d1, d2);
    int cl = 0, cr = 0;
    for(int i = l; i <= mid; i++)
        if(p[mid].x - p[i].x <= d)
            pl[cl++] = p[i];
    for(int i = mid+1; i <= r; i++)
        if(p[i].x - p[mid].x <= d)
            pr[cr++] = p[i];
    sort(pr, pr+cr, compy); 
    for(int i = 0; i < cl; i++)
    {
        int id = fd(0,cr-1, pl[i].y-d);
        for(int j = 0; j < 6 && id+j < cr; j++)
            d = min(d, dist(pl[i], pr[id+j]));
    }
    return d;
}
int main()
{
    int n;
    while(~scanf("%d", &n), n)
    {
        for(int i = 0; i < n; i++) scanf("%lf %lf", &p[i].x, &p[i].y);
        sort(p, p+n);
        double ans = solve(0, n-1);
        printf("%.2lf
", sqrt(ans)/2.0);
    }
    return 0; 
}