tarjan求强连通分量

转载自http://www.cnblogs.com/shadowland/p/5872257.html

一.算法简介

我们定义：

如果两个顶点可以相互通达，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

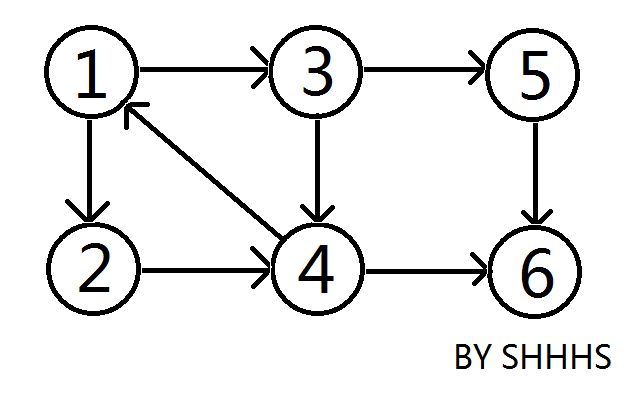
例如：在上图中，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 三个区域可以相互连通，称为这个图的强连通分量。

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

再Tarjan算法中，有如下定义。

DFN[ i ] : 在DFS中该节点被搜索的次序(时间戳)

LOW[ i ] : 为i或i的子树能够追溯到的最早的栈中节点的次序号

当DFN[ i ]==LOW[ i ]时，为i或i的子树可以构成一个强连通分量。

二.算法图示

以1为Tarjan 算法的起始点，如图

顺次DFS搜到节点6

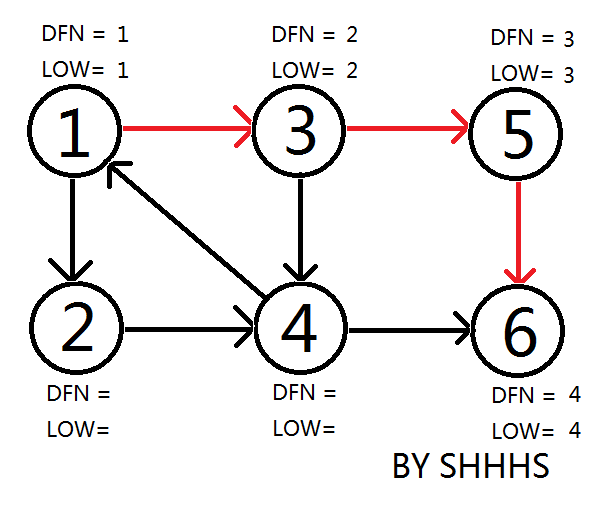
 回溯时发现LOW[ 5 ]==DFN[ 5 ] ,  LOW[ 6 ]==DFN[ 6 ] ,则{ 5 } , { 6 } 为两个强连通分量。回溯至3节点，拓展节点4.

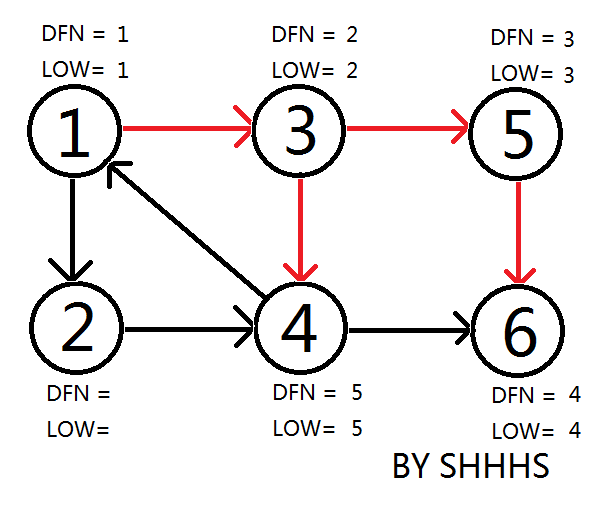
拓展节点1 ， 发现1再栈中更新LOW[ 4 ]，LOW[ 3 ] 的值为1

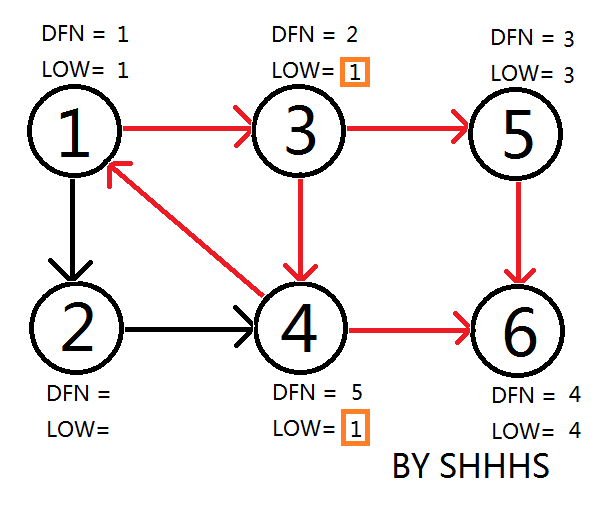
 回溯节点1，拓展节点2

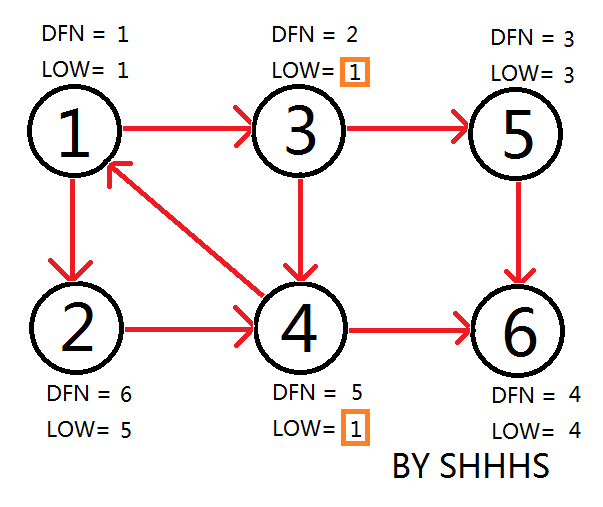
自此，Tarjan Algorithm 结束，{1 , 2 , 3 , 4 } , { 5 }　,  { 6 } 为图中的三个强连通分量。

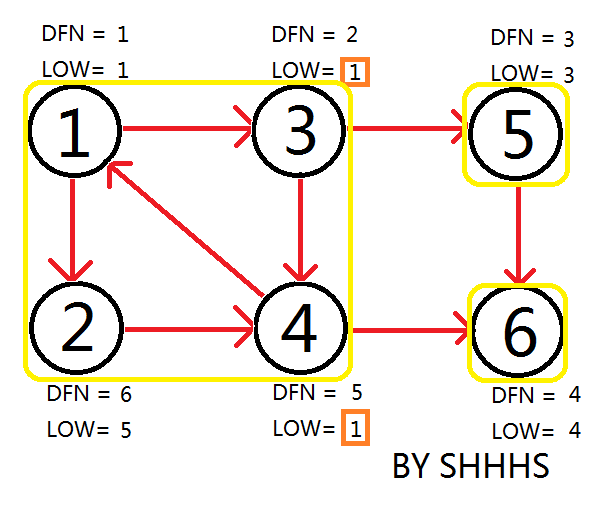
不难发现，Tarjan Algorithm 的时间复杂度为O(E+V).

代码：

#include<cstdio>
#include<algorithm>
using namespace std;
#define maxn 1005
struct Edge{
    int next,to;
}edge[maxn*maxn];
int fi[maxn],se,col[maxn],sc,sta[maxn],top,dfn[maxn],low[maxn],df;//col为每个点属于的强连通分量,sta为模拟的栈; 
bool vis[maxn];
inline void add_edge(int u,int v){
    edge[++se].next=fi[u],fi[u]=se,edge[se].to=v;
}
void Tarjan(int x){
    dfn[x]=low[x]=++df,vis[x]=1,sta[++top]=x;
    for(int i=fi[x];i;i=edge[i].next){
        int v=edge[i].to;
        if(!dfn[v])Tarjan(v),low[x]=min(low[x],low[v]);//没有遍历过 
        else if(vis[v])low[x]=min(low[x],dfn[v]);//不在栈内的要么是low[v]<dfn[x]，要么不互相连通 
    }
    if(dfn[x]==low[x]){//有一个强联通分量 
        vis[x]=0,col[x]=++sc;
        while(sta[top]!=x){
            col[sta[top]]=sc,vis[sta[top--]]=0;
        }
        top--;
    }
}
int main(){
    return 0;
}