部分树形DP的优化

ural1018. Binary Apple Tree

题目大意

有一棵n个节点的树,树上每个节点有一个值,选择m个节点使这些节点值的和最大
要求:如果选当前节点，则必须选它的父节点

解法：

我们设dp[i][j]为以i为根的树上留j个节点的最大值，转移方法如下

for(int j=min(q,size[x]);j>1;j--){//size表示子树的大小 
    for(int k=min(j-1,size[v]);k>0;k--){//因为父节点要保留所以j-k要>=1 
        dp[x][j]=max(dp[x][j],dp[v][k]+dp[x][j-k]);//v为x的子节点 
    }
}

复杂度O(n*m^2)

“金明的预算方案”加强版

题目大意

有一棵n个节点的树,树上每个节点有一个代价和一个价值,选择若干个节点使这些节点的价值最大并且代价不超过m
要求:如果选当前节点，则必须选它的父节点$nle 5000,mle 10000$

题解：

如果还像上一题那样考虑的话，dp[i][j]为以i为根的子树代价为j的最大价值,
共有m*n个状态,每个状态O(m)转移,复杂度O(m*m*n)，虽然达不到那么高，但也一定会超时

考虑优化

首先将所有节点后序遍历,p[i]保存dfs序为i的节点编号,
l[i]保存在i节点的子树之前遍历的最后一个dfs序,如下图

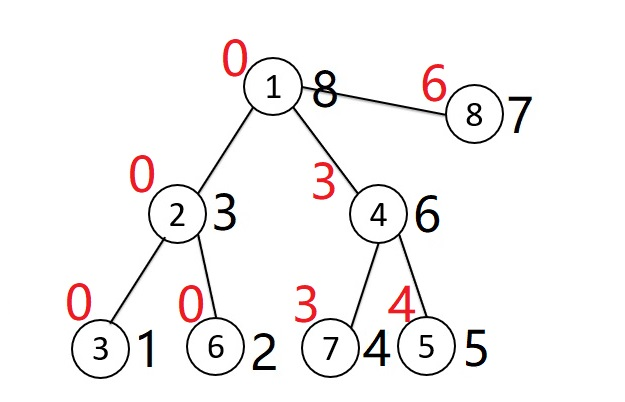
节点右侧的为节点的dfs序,左上角的为l的值:
如p[4]=7,l[7]=3代表7号节点dfs序为4，在7节点的子树之前遍历的最后一个dfs序为3

然后将dp[i][j]的意义改为前i个遍历的节点代价为j的最大值
dp[i][j]=max(dp[l[u]][j](当前节点不选，则子树都不能选),dp[i-1][j-v[u]]+w[u](选当前节点))   注：u=p[i];
于是状态转移变成O(1)了，时间复杂度O(n*m)

思考一下上一题是否也可以这样优化?

只需将dp[i][j]的意义改为前i个遍历的节点留j个的最大值即可，其他转移都一样