定义:
Treap,顾名思义,就是tree和heap的结合,既满足二叉搜索树的性质,又满足二叉堆的性质
但是一个要求节点值小于右儿子的值,一个要求节点值大于右儿子的值,显然不可能做到
那我们只能一个节点存两个值,一个满足二叉搜索树(BST)性质,一个满足二叉堆的性质:如下图
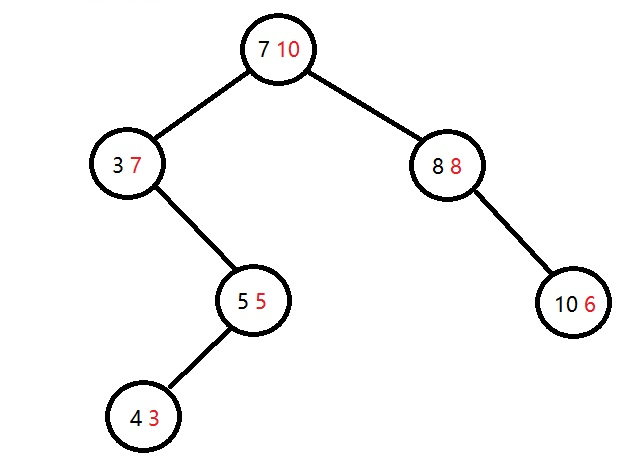
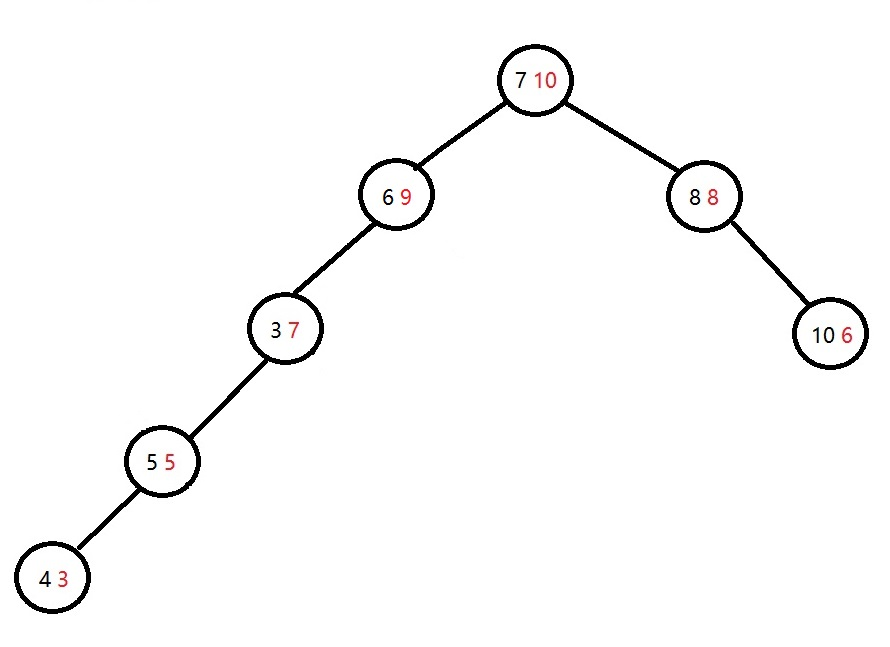
节点中黑色的值满足二叉搜索树的性质,红色的值满足二叉(大根)堆的性质。并且给定这些节点,这棵Treap是唯一的
用处:
那这个Treap到底有什么用呢?
我们知道二叉搜索树可以维护一个有序的序列期望插入删除期望复杂度O(logn)
但是如果是极限数据的话,二叉搜索树可能会退化成链表,复杂度变为O(n),相当于白用了
于是我们为了防止它退化成链表,就让每个节点维护两个数,使另一个数满足二叉堆的性质
使他可以自己平衡,成为平衡树,这就是Treap
具体操作
存储
struct Treap{ int key,prio,size,num;//key满足二叉搜索树,prio满足二叉堆,num是key值的数目,size是子树中num之和 Treap* son[2]; Treap(){ memset(this,0,sizeof(Treap)); } Treap(int k){ key=k,prio=random(),size=num=1,son[0]=son[1]=0; } }*root;
插入
我们对于每个要插入的数据配上一个随机生成的数,按照二叉搜索树的插入方法插入到树中
但是这就可能使Treap不满足二叉堆的性质了。如再上图中插入6 9就成了下面这样
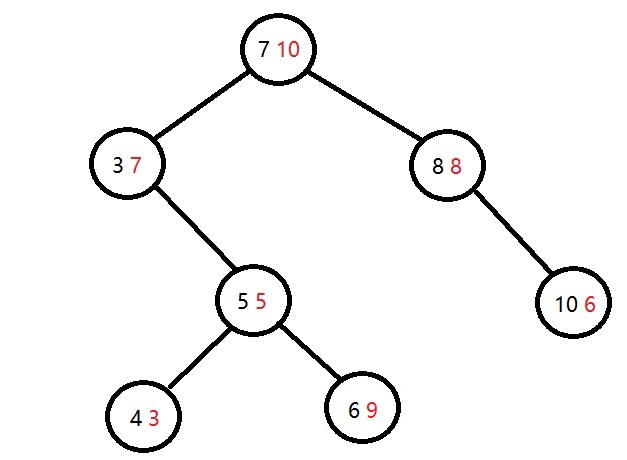
然后就是平衡树的精髓所在了——旋转
比如对于上面的Treap中不满足的子树5 5,我们可以让他向左旋转,就变成了这样
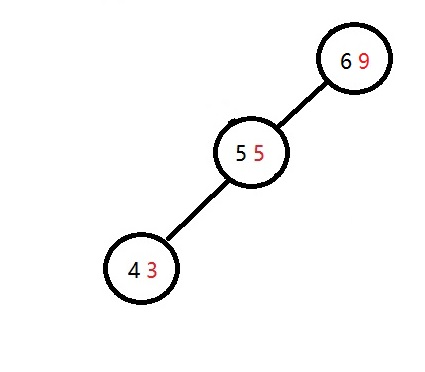
整棵树就是这样
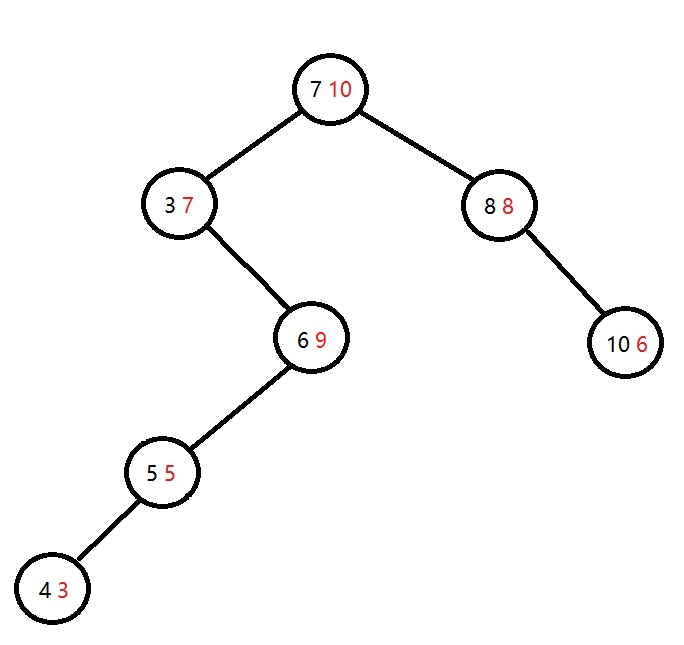
这时整棵树还不满足,并且如果只对3 7这颗子树进行简单的旋转就不行了(即它的右儿子(6 9)已经有了左儿子(5 5)),3 7不能直接旋转到6 9的左儿子
现在就需要一些技巧了,我们发现3 7的右儿子没了,但6 9多出个左儿子,并且6 9的左儿子满足3 7的右儿子,我们把5 5接到3 7的右儿子即可
这样整个插入操作就结束了
inline int random(){//生成随机数 static int seed=66; return seed=seed*48271LL%2147483647;//百度上说会把[0,2147483646]都生成一遍不会重复 }
void rotate(Treap *&x,int d){//旋转,d为旋转方向,0为左旋,1为右旋 Treap *y=x->son[d^1];//y指向要旋转到父节点的子节点 x->son[d^1]=y->son[d],y->son[d]=x;//更新指向关系 y->size=x->size;//更新size值 x->size=size(x->son[0])+size(x->son[1])+x->num; x=y;//别忘了将进入子树的指针指到y上 } void insert(Treap *&x,int key){//插入节点 if(x==NULL){//节点为空则直接创建一个节点 x=new Treap(key);return; } x->size++; if(key==x->key){x->num++;return;}//权值已经存在,则num++; int d=key>x->key; insert(x->son[d],key);//加入到子节点 if(x->prio < x->son[d]->prio)rotate(x,d^1);//别忘了旋转来满足堆的性质 }
代码中的size()是个宏,具体实现如下
#define size(x) (x!=NULL?x->size:0)
删除
Treap的删除也和BST差不多,大致分为3种情况:
- 如果结点x没有孩子节点,那么只需简单地将其删除,并修改父节点,用NULL来替换x;
- 如果结点x只有一个孩子,那么将这个孩子节点提升到x的位置,并修改x的父节点,用x的孩子替换x
- 如果结点x有2个孩子,那么找到孩子中prio值较大的旋转到子树的根,然后进入x所在的子树再按照这三种方法删除
void del(Treap *&x,int key){//删除节点 if(x->key!=key){ del(x->son[key>x->key],key);//进入子节点找权值为key的节点 x->size--;//总数减一 return; } //找到节点后 if(x->num>1){//如果插入不止一次,就num--即可 x->num--,x->size--;return; } Treap* p=x; if(x->son[0]==NULL)x=x->son[1],delete p;//左子节点为空,用右子节点(可能也为空)替代自己 else if(x->son[1]==NULL)x=x->son[0],delete p;//右子节点为空,用左子节点替代自己 else{ int d=x->son[0]->prio > x->son[1]->prio; rotate(x,d);//将prio值较大的旋转到上面 del(x,key);//进入x在的子树,再进行删除 } }
其他操作
这些基本和BST相同,就直接粘代码了
中序遍历
void mid_traversal(Treap* x){//中序遍历,即按照排序好的顺序输出 if(x->son[0])mid_traversal(x->son[0]); printf("%d ",x->key); if(x->son[1])mid_traversal(x->son[1]); }
求前驱和后继
int ans; void pre(Treap *x,int num){//求num的前驱(即小于num的最大的数) if(x==NULL)return; if(x->key<num)ans=x->key,pre(x->son[1],num); else pre(x->son[0],num); } void suc(Treap *x,int num){//求后继 if(x==NULL)return; if(x->key>num)ans=x->key,suc(x->son[0],num); else suc(x->son[1],num); }
查询排名为x的数
int query_key(Treap *x,int num){//求排第num的数 if(x==NULL)return 0; if(size(x->son[0])>=num)return query_key(x->son[0],num);//左子树大小大于等于num,在左子树中找排num的数即可 if(size(x->son[0])+x->num>=num)return x->key;//排第num的数是当前节点 return query_key(x->son[1],num-size(x->son[0])-x->num);//在右子树找排num-(左子树大小+当前节点大小)的数即可 }
查找有多少数比x要小
int query_id(Treap *x,int key){//求数列中比key小的有几个 if(x==NULL)return 0; if(x->key>key)return query_id(x->son[0],key);//当前节点的值大于key,求在左子树中的排名即可 if(x->key==key)return size(x->son[0]);//当前节点个数等于key,返回左子树大小 else return size(x->son[0])+x->num+query_id(x->son[1],key);//在右子树找,值要加上左子树大小和当前节点的大小 }
例题luoguP3369 【模板】普通平衡树(Treap/SBT)
#include<cstdio> #include<cstring> using namespace std; #define size(x) (x!=NULL?x->size:0) inline int random(){//生成随机数 static int seed=66; return seed=seed*48271LL%2147483647;//百度上说会把[0,2147483646]都生成一遍不会重复 } struct Treap{ int key,prio,size,num;//key满足二叉搜索树,prio满足二叉堆,num是key值的数目,size是子树中num之和 Treap* son[2]; Treap(){ memset(this,0,sizeof(Treap)); } Treap(int k){ key=k,prio=random(),size=num=1,son[0]=son[1]=0; } }*root; void rotate(Treap *&x,int d){//旋转,d为旋转方向,0为左旋,1为右旋 Treap *y=x->son[d^1];//y指向要旋转到父节点的子节点 x->son[d^1]=y->son[d],y->son[d]=x;//更新指向关系 y->size=x->size;//更新size值 x->size=size(x->son[0])+size(x->son[1])+x->num; x=y;//别忘了将进入子树的指针指到y上 } void insert(Treap *&x,int key){//插入节点 if(x==NULL){//节点为空则直接创建一个节点 x=new Treap(key);return; } x->size++; if(key==x->key){x->num++;return;}//权值已经存在,则num++; int d=key>x->key; insert(x->son[d],key);//加入到子节点 if(x->prio < x->son[d]->prio)rotate(x,d^1);//别忘了旋转来满足堆的性质 } void del(Treap *&x,int key){//删除节点 if(x->key!=key){ del(x->son[key>x->key],key);//进入子节点找权值为key的节点 x->size--;//总数减一 return; } //找到节点后 if(x->num>1){//如果插入不止一次,就num--即可 x->num--,x->size--;return; } Treap* p=x; if(x->son[0]==NULL)x=x->son[1],delete p;//左子节点为空,用右子节点(可能也为空)替代自己 else if(x->son[1]==NULL)x=x->son[0],delete p;//右子节点为空,用左子节点替代自己 else{ int d=x->son[0]->prio > x->son[1]->prio; rotate(x,d);//将prio值较大的旋转到上面 del(x,key);//进入x在的子树,再进行删除 } } int query_id(Treap *x,int key){//求数列中比key小的有几个 if(x==NULL)return 0; if(x->key>key)return query_id(x->son[0],key);//当前节点的值大于key,求在左子树中的排名即可 if(x->key==key)return size(x->son[0]);//当前节点个数等于key,返回左子树大小 else return size(x->son[0])+x->num+query_id(x->son[1],key);//在右子树找,值要加上左子树大小和当前节点的大小 } int query_key(Treap *x,int num){//求排第num的数 if(x==NULL)return 0; if(size(x->son[0])>=num)return query_key(x->son[0],num);//左子树大小大于等于num,在左子树中找排num的数即可 if(size(x->son[0])+x->num>=num)return x->key;//排第num的数是当前节点 return query_key(x->son[1],num-size(x->son[0])-x->num);//在右子树找排num-(左子树大小+当前节点大小)的数即可 } int ans; void pre(Treap *x,int num){//求num的前驱(即小于num的最大的数) if(x==NULL)return; if(x->key<num)ans=x->key,pre(x->son[1],num); else pre(x->son[0],num); } void suc(Treap *x,int num){//求后继 if(x==NULL)return; if(x->key>num)ans=x->key,suc(x->son[0],num); else suc(x->son[1],num); } void mid_traversal(Treap* x){//中序遍历,即按照排序好的顺序输出 if(x->son[0])mid_traversal(x->son[0]); printf("%d ",x->key); if(x->son[1])mid_traversal(x->son[1]); } int main(){ int n,x,y;scanf("%d",&n); while(n--){ scanf("%d%d",&x,&y); switch(x){ case 1: insert(root,y); break; case 2: del(root,y); break; case 3: printf("%d ",query_id(root,y)+1); break; case 4: printf("%d ",query_key(root,y)); break; case 5: pre(root,y);printf("%d ",ans); break; default: suc(root,y);printf("%d ",ans); } } return 0; }