AVL树

AVL树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis，是一种高度平衡的自平衡二叉查找树

它的查找、插入和删除在平均和最坏情况下都是O（log n），这得益于它的性质：
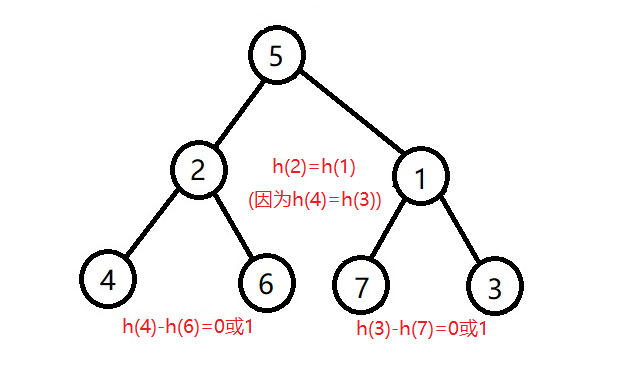
在满足二叉查找树的性质情况下，还满足每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1

具体实现

节点存储

struct AVL{
    int key,height,num,size;//size只有在求排名和第k大时才需要,num在有重复加入时才需要,其它AVL中可以不用
    AVL *son[2];
    AVL(){
        memset(this,0,sizeof(AVL));
    }
    AVL(int x){
        key=x,size=height=num=1,son[0]=son[1]=0;
    }
}*root;

在插入和删除和操作后,AVL树可能不满足节点平衡因子最多为1的性质，这时就需要对AVL树进行平衡维护

平衡维护的基本操作就是旋转

旋转操作和其他平衡树都一样

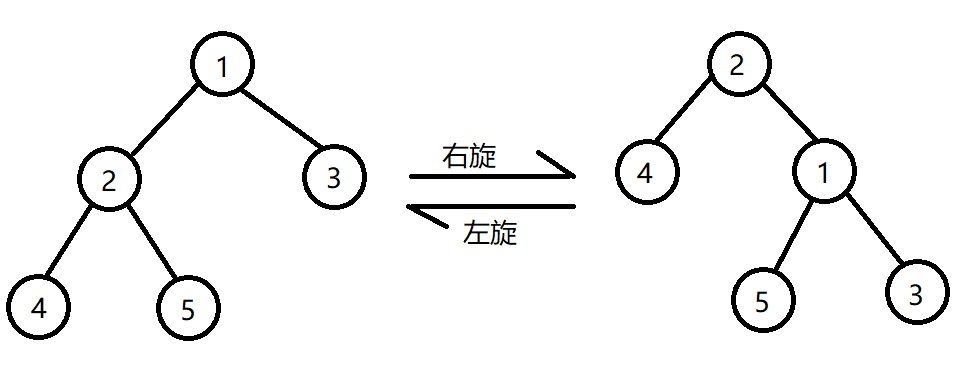
#define getheight(x) (x?x->height:0)
#define size(x) (x?x->size:0)
void rotate(AVL *&x,int d){
    AVL *p=x->son[d^1];
    x->son[d^1]=p->son[d],p->son[d]=x;//更新指向关系 
    x->height=max(getheight(x->son[0]),getheight(x->son[1]))+1,//更新高度和size 
    p->height=max(getheight(p->son[0]),getheight(p->son[1]))+1;
    p->size=x->size,x->size=x->num+size(x->son[0])+size(x->son[1]);
}

平衡维护

AVL在插入或删除操作后，造成的不平衡大致分为两种情况(左右对称算一种,这里以左子树高度大为例)：

1. 左子树高度-右子树高度>1,并且左子节点的左子树高度>左子节点的右子树高度，如下图:
   
   其中3，4，5都是AVL子树，只是子节点被省略

   这时只用右旋子树1即可
   

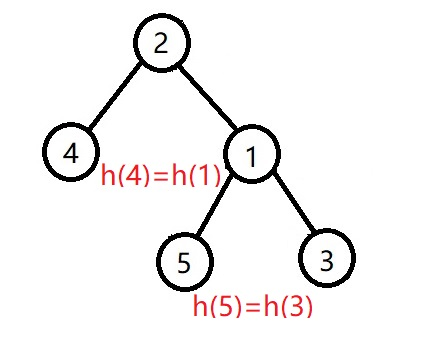
2. 左子树高度-右子树高度>1,并且左子节点的右子树高度>左子节点的左子树高度，如下图:
   

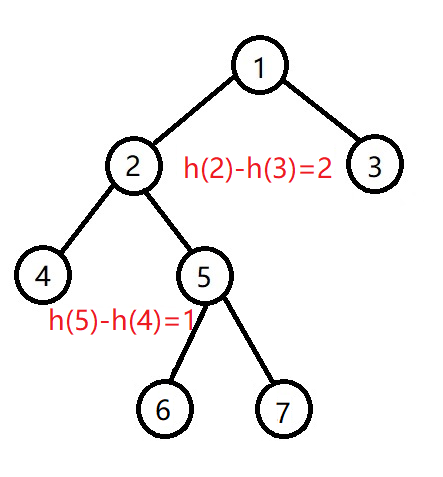
   这时要先左旋子树2
   

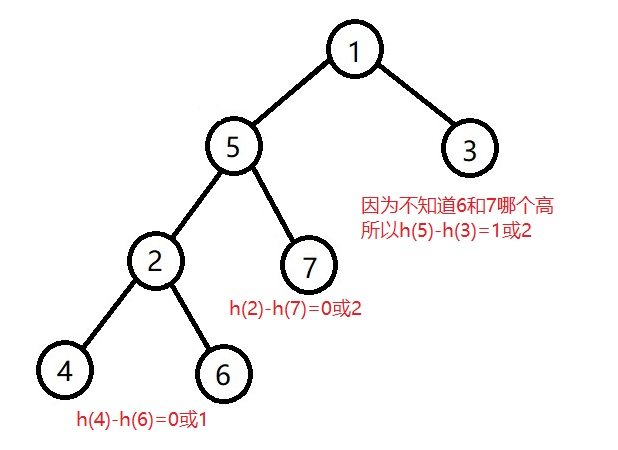
   然后再右旋子树1
   

插入和删除(和二叉查找树一样,结束后平衡一下即可)

void insert(AVL *&x,int key){//插入key 
    if(!x){
        x=new AVL(key);return;
    }
    x->size++;
    if(key==x->key){x->num++;return;}
    insert(x->son[key>x->key],key);
    maintain(x);
}
void del(AVL *&x,int key){//删除key 
    if(!x)return;
    if(x->key!=key){
        del(x->son[x->key<key],key);
        x->size=size(x->son[0])+size(x->son[1])+x->num,maintain(x);
        return;
    } 
    x->size--;
    if(x->num>1){x->num--;return;}
    AVL *p=x;
    if(x->son[0]==NULL)x=x->son[1],delete p;
    else if(x->son[1]==NULL)x=x->son[0],delete p;
    else{//用后继替换当前节点，删除后继 
        p=x->son[1];
        while(p->son[0]){
            p=p->son[0];
        }
        x->num=p->num,x->key=p->key,p->num=1,del(x->son[1],p->key);
    }
}

其他操作

int query_id(AVL *x,int key){//求数列中比key小的有几个 
    if(!x)return 0;
    if(x->key>key)return query_id(x->son[0],key);
    if(x->key==key)return size(x->son[0]);
    return query_id(x->son[1],key)+size(x->son[0])+x->num;
}
int query_k(AVL *x,int k){//求排第k的数 
    if(!x)return 0;
    if(size(x->son[0])>=k)return query_k(x->son[0],k);
    if(size(x->son[0])+x->num>=k)return x->key;
    return query_k(x->son[1],k-size(x->son[0])-x->num);
}
int ans;
void pre(AVL *x,int num){//求num的前驱(即小于num的最大的数)，并存在ans里 
    if(!x)return;
    if(x->key<num)ans=x->key,pre(x->son[1],num);
    else pre(x->son[0],num);
}
void suc(AVL *x,int num){//求后继 
    if(!x)return;
    if(x->key>num)ans=x->key,suc(x->son[0],num);
    else suc(x->son[1],num);
}
void mid_traversal(AVL *x){//中序遍历
    if(x->son[0])mid_traversal(x->son[0]);
    printf("%d ",x->key);
    if(x->son[1])mid_traversal(x->son[1]);
}

例题luoguP3369 【模板】普通平衡树（Treap/SBT）

#include<cstdio>
#include<cstring>
#include<algorithm> 
#include<cmath>
using namespace std;
#define getheight(x) (x?x->height:0)
#define size(x) (x?x->size:0)
struct AVL{
    int key,height,num,size;//size只有在求排名和第k大时才需要,num在有重复加入时才需要,其它AVL中可以不用
    AVL *son[2];
    AVL(){
        memset(this,0,sizeof(AVL));
    }
    AVL(int x){
        key=x,size=height=num=1,son[0]=son[1]=0;
    }
}*root;
void rotate(AVL *&x,int d){
    AVL *p=x->son[d^1];
    x->son[d^1]=p->son[d],p->son[d]=x;//更新指向关系 
    x->height=max(getheight(x->son[0]),getheight(x->son[1]))+1,//更新高度和size 
    p->height=max(getheight(p->son[0]),getheight(p->son[1]))+1;
    p->size=x->size,x->size=x->num+size(x->son[0])+size(x->son[1]);
}
void maintain(AVL *&x){//平衡操作 
    if(abs(getheight(x->son[0])-getheight(x->son[1]))<2)return;
    int d=getheight(x->son[0])<getheight(x->son[1]);
    if(getheight(x->son[d]->son[d])>getheight(x->son[d]->son[d^1]))rotate(x,d^1);
    else rotate(x->son[d],d),rotate(x,d^1);
} 
void insert(AVL *&x,int key){//插入key 
    if(!x){
        x=new AVL(key);return;
    }
    x->size++;
    if(key==x->key){x->num++;return;}
    insert(x->son[key>x->key],key);
    maintain(x);
}
void del(AVL *&x,int key){//删除key 
    if(!x)return;
    if(x->key!=key){
        del(x->son[x->key<key],key);
        x->size=size(x->son[0])+size(x->son[1])+x->num,maintain(x);
        return;
    } 
    x->size--;
    if(x->num>1){x->num--;return;}
    AVL *p=x;
    if(x->son[0]==NULL)x=x->son[1],delete p;
    else if(x->son[1]==NULL)x=x->son[0],delete p;
    else{//用后继替换当前节点，删除后继 
        p=x->son[1];
        while(p->son[0]){
            p=p->son[0];
        }
        x->num=p->num,x->key=p->key,p->num=1,del(x->son[1],p->key);
    }
}
int query_id(AVL *x,int key){//求数列中比key小的有几个 
    if(!x)return 0;
    if(x->key>key)return query_id(x->son[0],key);
    if(x->key==key)return size(x->son[0]);
    return query_id(x->son[1],key)+size(x->son[0])+x->num;
}
int query_k(AVL *x,int k){//求排第k的数 
    if(!x)return 0;
    if(size(x->son[0])>=k)return query_k(x->son[0],k);
    if(size(x->son[0])+x->num>=k)return x->key;
    return query_k(x->son[1],k-size(x->son[0])-x->num);
}
int ans;
void pre(AVL *x,int num){//求num的前驱(即小于num的最大的数)，并存在ans里 
    if(!x)return;
    if(x->key<num)ans=x->key,pre(x->son[1],num);
    else pre(x->son[0],num);
}
void suc(AVL *x,int num){//求后继 
    if(!x)return;
    if(x->key>num)ans=x->key,suc(x->son[0],num);
    else suc(x->son[1],num);
}
void mid_traversal(AVL *x){//中序遍历
    if(x->son[0])mid_traversal(x->son[0]);
    printf("%d ",x->key);
    if(x->son[1])mid_traversal(x->son[1]);
}
int main(){
    int n,x,y;scanf("%d",&n);
    while(n--){
        scanf("%d%d",&x,&y);
        switch(x){
            case 1:
                insert(root,y);
                break;
            case 2:
                del(root,y);
                break;
            case 3:
                printf("%d
",query_id(root,y)+1);
                break;
            case 4:
                printf("%d
",query_k(root,y));
                break;
            case 5:
                pre(root,y);printf("%d
",ans);
                break;
            default:
                suc(root,y);printf("%d
",ans);
            
        }
    }
    return 0;
}