Konig定理
由匈牙利数学家柯尼希(D.Konig)于1913年首先陈述的定理。
定理的内容:在0-1矩阵中,1的最大独立集合最小覆盖包含的元素个数相同,等价地,二分图中的最大匹配数等于这个图中的最小点覆盖数。
证明:
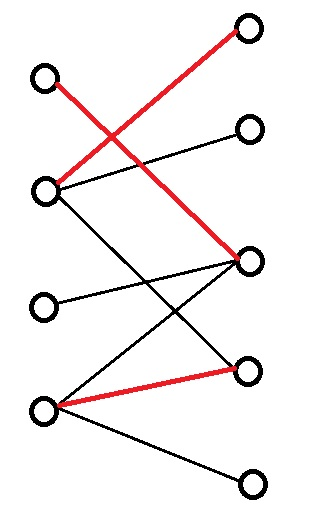
对于上面的二分图,它的最大匹配(不唯一)已经用红线标出来了,
然后我们对于右边或左边(这里按右边为例)没有匹配的点,我们从它出发走交替路(这里有介绍),会经过若干节点
将所有从右边没有匹配的点开始的交替路上的所有的点标注起来(如下图标蓝的点)
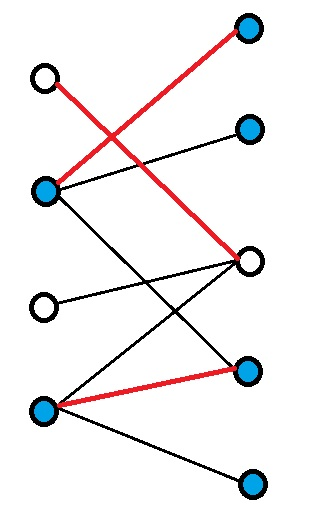
可以证明左边所有被标注的点都是被匹配的点(否则从未匹配的点到未匹配的点的交替路就是增广路)
右边所有没有被标注的点都是被匹配的点(或是没连任何边的点,可以忽略。否则可以从它开始走任意非匹配边,它就会被标注)
这些点就是最小覆盖点集(被标红)
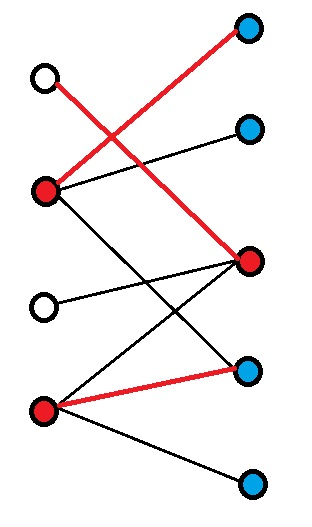
因为对于所有右边被标注的点连的边,其左边的点都被标注了,会被覆盖
假设左边的点是不是匹配点且没被标注,则当前边一定不是匹配边,可以加入交替路中,所以假设不成立
假设左边的点是匹配点且没被标注,则当前边一定是匹配边且不在交替路中,那么右边的这个点也是匹配点且被标记,那么右边的这个点已经连了一个在交替路中的匹配边,但一个点最多会有一个匹配边,所以假设不成立
对于所有左边没被标注的点连的边,其右边的点都没被标注
假设右边的点是匹配点且被标注,则当前边一定不是匹配边,可以加入交替路中,所以假设不成立
假设右边的点不是匹配点且被标注,则当前边一定不是匹配边,可以加入交替路中,所以假设不成立
所以所有边都被覆盖了