1. 背景介绍
2. L1正则化法
L1正则化法很简单，在GD，SGD，OGD中都会用到，其对权重的更新方式如下：
但是，在线计算的每次迭代过程中，仅仅靠几个float类型的数相加，是很难得到0的，所以说很难得到稀疏解。
3. 简单截断法
为了得到稀疏的特征权重，最简单粗暴的方式就是设定一个阈值，当的某维度上系数小于这个阈值时将其设置为0（称作简单截断）。其以为窗口，当/不为整数时采用标准的SGD进行迭代，当/为整数时，采用如下权重更新方式：
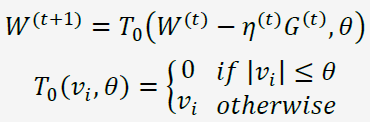
这种方法实现起来很简单，也容易理解。但实际中（尤其在OGD里面）的某个系数比较小可能是因为该维度训练不足引起的，简单进行截断会造成这部分特征的丢失。
4. 梯度截断法（TG）
上述的简单截断法被TG的作者形容为too aggressive，因此TG在此基础上进行了改进，同样是采用截断的方式，但是比较不那么粗暴。采用相同的方式表示为：
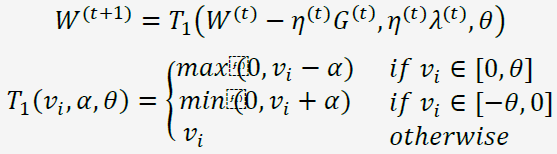
首先看一下梯度截断法与简单截断法的关系：
从图中可以看出，如果令α=θ的话，则TG退化成简单截断法。
梯度截断法与L1正则法的关系：
令
和
，则TG的特征权重更新公式变为：
此时，TG退化为L1正则法。
5. FOBOS
前向后向切分（FOBOS, Forward-Backward Splitting）是由John Duchi和Yoram Singer提出的。FOBOS的权重更新公式为：
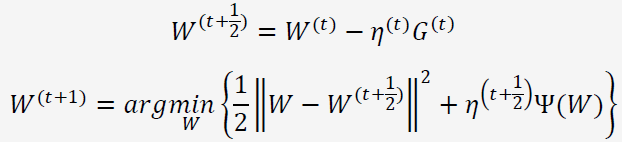
前一个步骤是一个标准的梯度下降步骤，后一个步骤可以理解为对梯度下降的结果进行微调。
观察第二个步骤，发现对的微调也分为两部分：(1) 前一部分保证微调发生在梯度下降结果的附近；(2)后一部分则用于处理正则化，产生稀疏性。
通过将两个公式相结合，我们可以得到如下的闭式解：
可以看到，特征权重不仅仅与迭代前的状态有关，而且与迭代后的状态有关。可能这就是FOBOS名称的由来。
L1-FOBOS：
将FOBOS公式中的正则化项选择为L1正则。经过一番公式推导，可以得到L1-FOBOS的权重更新公式为：
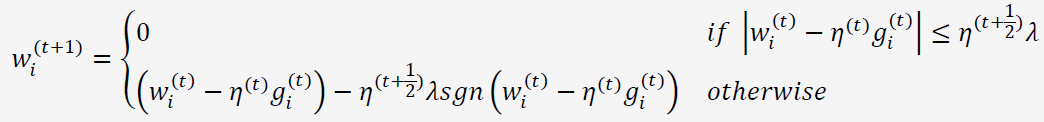
即，当一条样本产生的梯度不足以令对应维度上的权重值发生足够大的变化，认为在本次更新后该维度不够重要，应当令其权重为0。
可以发现，令
时，L1-FOBOS与TG完全一致，我们可以认为L1-FOBOS是TG在特定条件下的特殊形式。
6. RDA
不论怎样，简单截断、TG、FOBOS都还是建立在SGD的基础之上的，属于梯度下降类型的方法，这类型方法的优点就是精度比较高，并且TG、FOBOS也都能在稀疏性上得到提升。但是有些其它类型的算法，例如RDA，是从另一个方面来求解Online Optimization并且更有效地提升了特征权重的稀疏性。
正则对偶平均（RDA, Regularized Dual Averaging）是微软十年的研究成果，RDA是Simple Dual Averaging Scheme一个扩展，由Lin Xiao发表于2010年。
RDA的权重更新公式如下：
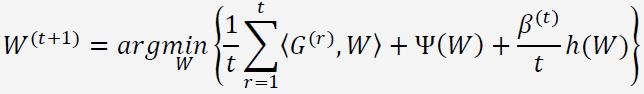
公式中包含了3个部分：（1）之前所有梯度（或次梯度）的平均值。（2）正则项。（3）额外正则项，严格凸函数。
L1-RDA：
将RDA公式中的正则化项选择为L1正则。经过一番公式推导，可以得到L1-RDA的权重更新公式为：
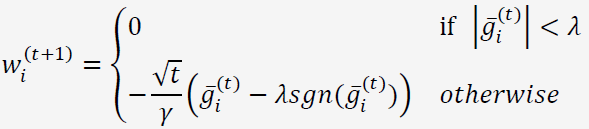
我们发现，当某个维度上累积梯度平均值的绝对值小于一个固定的阈值的时候，该维度权重将被置0，特征权重的稀疏性由此产生。
L1-RDA与L1-FOBOS的比较：
我们看到了L1-FOBOS实际上是TG的一种特殊形式，在L1-FOBOS中，进行“截断”的判定条件是
。通常会定义为与
正相关的函数
，因此L1-FOBOS的“截断阈值”随着的增加，这个阈值会逐渐降低。
相比较而言，L1-RDA的“截断阈值”为，是一个常数，并不随着而变化，因此可以认为L1-RDA比L1-FOBOS在截断判定上更加aggressive，这种性质使得L1-RDA更容易产生稀疏性；此外，RDA中判定对象是梯度的累加平均值
，不同于TG或L1-FOBOS中针对单次梯度计算的结果进行判定，避免了由于某些维度由于训练不足导致截断的问题。并且通过调节一个参数，很容易在精度和稀疏性上进行权衡。
7. FTRL
我们从原理上定性比较了L1-FOBOS和L1-RDA在稀疏性上的表现。有实验证明，L1-FOBOS这一类基于梯度下降的方法有比较高的精度，但是L1-RDA却能在损失一定精度的情况下产生更好的稀疏性。那么这两者的优点能不能在一个算法上体现出来？这就是FTRL要解决的问题。
FTRL（Follow the Regularized Leader）是由Google的H. Brendan McMahan在2010年提出的，后来在2011年发表了一篇关于FTRL和AOGD、FOBOS、RDA比较的论文，2013年又和Gary Holt, D. Sculley, Michael Young等人发表了一篇关于FTRL工程化实现的论文。
L1-FOBOS和L1-RDA在形式上的统一：
经过公式推导，我们可以得到在形式上统一的L1-FOBOS和L1-RDA：
可以看出L1-FOBOS和L1-RDA的区别在于：(1) 前者对计算的是单次梯度以及L1正则项只考虑当前模的贡献，而后者采用了累加的处理方式；(2) 前者的第三项限制的变化不能离已迭代过的解太远，而后者则限制不能离0点太远。
FTRL算法原理：
FTRL综合考虑了FOBOS和RDA对于正则项和限制的区别，其特征权重的更新公式为：
公式看上去很复杂，更新特征权重貌似非常困难的样子。不妨将其进行改写，令
，可以转化为：
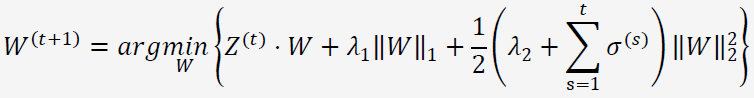
最终，对每个维度，权重更新公式为：
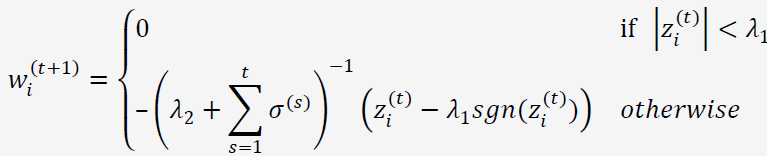
8. FTRL工程实现中的一些技巧
8-1. Per-Coordinate Learning Rates：
在一个标准的OGD里面使用的是一个全局的学习率策略，这个策略保证了学习率是一个正的非增长序列，对于每一个特征维度都是一样的。
考虑特征维度的变化率：如果特征1比特征2的变化更快，那么在维度1上的学习率应该下降得更快。我们很容易就可以想到可以用某个维度上梯度分量来反映这种变化率。在FTRL中，维度i上的学习率是这样计算的：
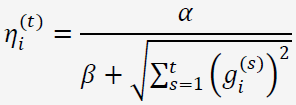
（1）Per-Coordinate的方式就是对每个不同的特征，根据该特征在样本中出现的次数来推算它的学习率。
（2）一个特征，如果出现的次数多，那么模型在该特征上学到的参数就已经比较可信了，所以学习率可以不用那么高。
（3）而对于出现次数少的特征，认为在这个特征上的参数还没有学完全，所以要保持较高的学习率来使之尽快适应新的数据。
8-2. 降低训练模型时的内存：
8-2-1. Probabilistic Feature Inclusion
1. 在广告点击预估场景下，是特别特别高维的数据，在这种数据中，很大一部分特征是只出现一次的，此时，如果想要降低模型的尺寸，即减少模型中特征的数目。
2. 直观上看，我们应该先读取一遍数据，然后把出现次数小于k次的特征删掉，但显然，这种方式对于online learning很有问题，而且将数据读取两遍也是极耗时间的,不可行。
3. 本文介绍的是概率法，使用随机的方式将特征添加进模型，有两种代表性的方法：
（1）Poisson Inclusion，这种方法，对每个特征，如果它没在模型中出现过，那么以概率p将其加入到模型中。直观上，这种方法就会将出现次数多的特征加入到模型中。
（2）Bloom Filter Inclusion, 使用counting Bloom filter来对特征进行检测，如果一个特征出现了超过n次，那么就将该特征添加进模型。
8-2-2. Encoding Values with Fewer Bits
1. 对于OGD来说，使用32位或64位的浮点数太奢侈了，因为训练好的模型中，绝大部分的参数的区间是在[-2,2]中的。所以，为了节省内存，使用q2.13的encode方法。
2. 在这种方法中，1bit用来表示正负， 2bit用来表示整数部分，13bit用来表示小数部分，一共16bit。
3. 实验表明，相对于64bit浮点数来说，使用q2.13浮点编码方法可以只使用25%的内存，而AucLoss几乎没有变化。
8-2-3. A Single Value Structure
1. 有些时候，需要训练大量的模型，而这些模型的区别仅仅是添加或删除一些特征。（前提）
2. 可以采用这样的方法，即若干模型共享的特征维度上，只存储1个系数权重值，而不是对每个模型都保存一个值。另外还需要对这个特征被哪些模型使用做一个标记位数组。
3. 更新参数的时候，对一个样本，不同的模型会对不同维度的权重计算出多个更新值。然后对一个特征维度，使用共享该特征的所有模型的更新值的平均值来进行更新。
8-2-4. SubSampling Training Data
1. 在实际中，CTR远小于50%，所以正样本更加有价值。通过对训练数据集进行降采样，可以大大减小训练数据集的大小。
2. 正样本全部采样（至少有一个广告被点击的query数据），负样本使用一个比例r采样（完全没有广告被点击的query数据）。但是直接在这种采样上进行训练，会导致比较大的biased prediction。
3. 解决办法：训练的时候，对样本再乘一个权重。权重直接乘到loss上面，从而梯度也会乘以这个权重。
8-3. Confidence Estimates：
在很多应用中，只预测广告的CTR还是不够的，还需要有一种指标去衡量这种预测的置信度。
（1）本文提出一种uncertainty score来衡量不确定性。
（2）对于每个特征，都会记录一个counter，counter的大小决定着该特征的学习速率，学习速率越小则表示该特征越可信。
（3）uncertainty score的计算在模型预测的同时能够给出。
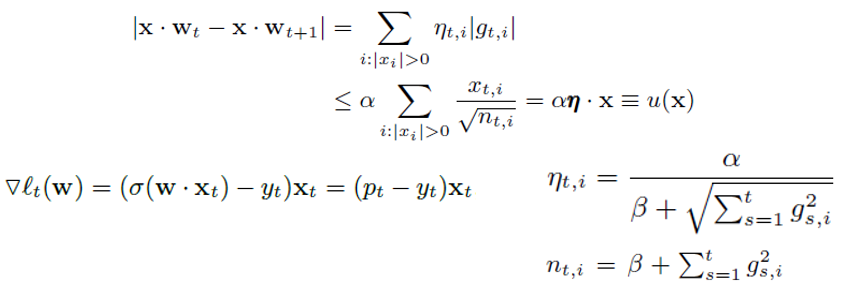
实验：
（1）使用一个ground truth模型作为基线model,称之为m1。
（2）使用m1对数据进行预测，得到每个样本的CTR。
（3）丢弃掉原来的类别标记，使用m1预测的结果作为真实值。
（4）在新数据上运行起FTRL，得到模型m2。
（5）m2和m1的预测值进行比较，得到错误et。
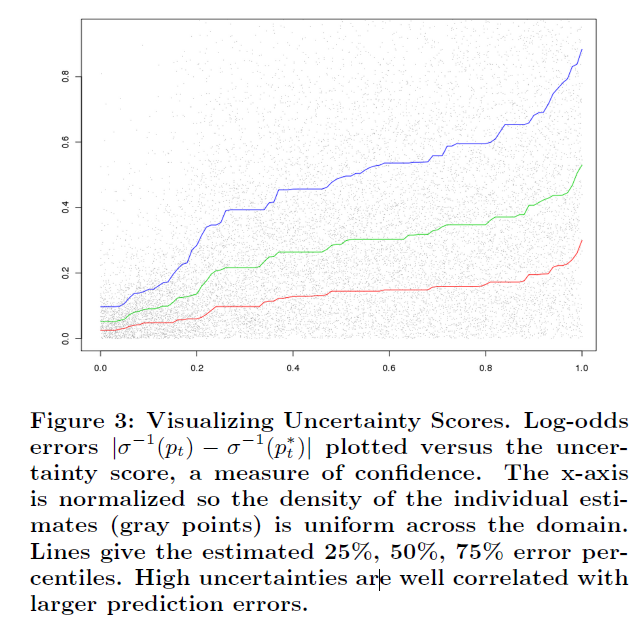
（6）m2运行时同时计算出u(x)。
（7）得到u(x)和et的关系，如图所示：
8-4. 另外，还有一些没有成功的实验尝试：
（1）Aggressive Feature Hashing
即允许哈希冲突，将一些不同的feature映射到同一个槽位。这样可以降低模型尺寸，但实验表明，一定会有效果损失。
（2）Dropout
对每一个样本，按照一定的概率p来随机丢掉特征，有利于泛化，增强模型的鲁棒性。这种方法在视觉方面用的比较多。在实验中，将drop rate从0.1调到0.5,发现都没有效果。分析原因，可能是广告数据和图像数据的分布不同所致，图像数据是紧密数据，各维度特征很可能是相关的；而广告数据是稀疏且噪声较大，这样做直接损失了较多信息。
（3）Feature Bagging
训练k个模型，每个模型用全部特征的一个子集，这些模型所用到的特征是overlapping的。然后用这k个模型的预测的平均值作为评测结果。发现并没有用。
（4）Feature Vector Normalization
将样本归一化，尽管其他的文献中有结果，发现在本文的实验中也是没有用。
9. 参考文献
1. Ad Click Prediction: a View from the Trenches
2. 在线最优化求解(Online Optimization)
版权声明：
本文由笨兔勿应所有，发布于http://www.cnblogs.com/bentuwuying。如果转载，请注明出处，在未经作者同意下将本文用于商业用途，将追究其法律责任。