Leetcode上一共出现了6道炒股问题:一个数组代表一支股票每天的价格,买了股票再卖出算一次交易,多个交易不能交叉,即只能卖了股票之后才能再买。求最大收益。
Leetcode上有一篇post介绍了一种通用的针对这类问题的解法,值得参考。
以下是我总结的每个问题比较容易理解的方法。
1.Best Time to Buy and Sell Stock 交易至多一次
这道题可以转化为求最大子数列问题。例如$[1, 7, 4, 11]$,可以转换为$[0, 6, -3, 7]$,然后计算该数组的最大子数列和即可,如果为负,返回0。
int maxProfit(vector<int>& prices) { int maxCur = 0, maxSoFar = 0; for(int i = 1; i < prices.size(); ++i){ maxCur = max(0, maxCur + prices[i] - prices[i - 1]); maxSoFar = max(maxSoFar, maxCur); } return maxSoFar; }
2.Best Time to Buy and Sell Stock II 交易任意多次
遍历数组,只要$prices[i] > prices[i-1]$,$maxprofit += prices[i] - prices[i -1]$
int maxProfit(vector<int>& prices) { int maxprofit = 0; for(int i = 1; i < prices.size(); ++i){ if(prices[i] > prices[i - 1]) maxprofit += prices[i] - prices[i - 1]; } return maxprofit; }
3.Best Time to Buy and Sell Stock III 至多交易两次
分析见4
int maxProfit(vector<int>& prices) { int n = prices.size(); if(n <= 1) return 0; vector<vector<int>> dp(3, vector<int>(n, 0)); for(int i = 1; i <= 2; ++i){ int tmpMax = dp[i - 1][0] - prices[0]; for(int j = 1; j < n; ++j){ dp[i][j] = max(dp[i][j - 1], prices[j] + tmpMax); tmpMax = max(tmpMax, dp[i - 1][j] - prices[j]); } } return dp[2][n - 1]; }
4.Best Time to Buy and Sell Stock IV 至多交易k次
int maxProfit(int k, vector<int>& prices) { int n = prices.size(); if(n < 2) return 0; //如果 k >= n/2,则问题转化为可以交易任意多次,用II的方法来防止TLE if(k >= n / 2){ int maxPro = 0; for(int i = 1; i < prices.size(); ++i){ if(prices[i] > prices[i - 1]) maxPro += prices[i] - prices[i - 1]; } return maxPro; } //dp[i][j]represents the max profit up until prices[j] (Note: NOT ending with prices[j]) using at most i transactions. //dp[i][j] = max(dp[i][j-1], prices[j] - prices[m] + dp[i-1][m]) {m in range of [0, j-1]} // = max(dp[i][j-1], prices[j] + max(dp[i-1][m] - prices[m])) //dp[0][j] = 0; 0 times transation makes 0 profit //dp[i][0] = 0; if there is only one price data point you can't make any money no matter how many times you can trade vector<vector<int>> dp(k + 1, vector<int>(n, 0)); for(int i = 1; i <= k; ++i){ int tmpMax = dp[i - 1][0] - prices[0]; for(int j = 1; j < n; ++j){ dp[i][j] = max(dp[i][j - 1], prices[j] + tmpMax); tmpMax = max(tmpMax, dp[i - 1][j] - prices[j]); } } return dp[k][n - 1]; }
5.Best Time to Buy and Sell Stock with Cooldown 卖了股票之后第二天不能买入(cooldown 1 day)
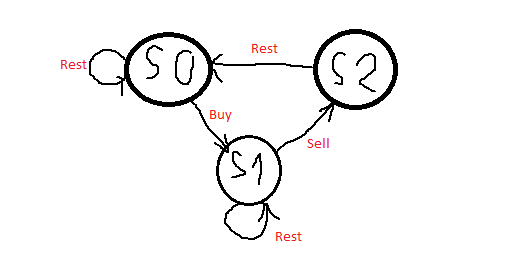
根据所能采取的动作,共有三种状态:$s0, s1, s2$, 在每个状态的第i天的收益为:
s0[i] = max(s0[i - 1], s2[i - 1]); // Stay at s0, or rest from s2 s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]); // Stay at s1, or buy from s0 s2[i] = s1[i - 1] + prices[i]; // Only one way from s1
初始状态:
s0[0] = 0; // At the start, you don't have any stock if you just rest s1[0] = -prices[0]; // After buy, you should have -prices[0] profit. Be positive! s2[0] = INT_MIN; // Lower base case
Code:
int maxProfit(vector<int>& prices) { int n = prices.size(); if(n < 2) return 0; vector<int> s0(n); vector<int> s1(n); vector<int> s2(n); s0[0] = 0; s1[0] = -prices[0]; s2[0] = INT_MIN; for(int i = 1; i < n; ++i){ s0[i] = max(s0[i - 1], s2[i - 1]); s1[i] = max(s1[i - 1], s0[i - 1] - prices[i]); s2[i] = s1[i - 1] + prices[i]; } return max(s0[n - 1], s2[n - 1]); }
6.Best Time to Buy and Sell Stock with Transaction Fee 可以交易任意多次,但每次交易都会有交易费用fee
$cash$表示第$i$天手中没有股票的最大收益
$hold$表示第$i$天手中有股票的最大收益
则在第$i+1$天,可以
卖出手中的股票:$cash = max(cash, hold + prices[i] -fee)$
或者买入股票:$hold = max(hold, cash - prices[i])$
最后cash就是最大收益。
We can transform $cash$ first without using temporary variables because selling and buying on the same day can't be better than just continuing to hold the stock.
int maxProfit(vector<int>& prices, int fee) { int cash = 0, hold = -prices[0]; for(int i = 1; i < prices.size(); ++i){ cash = max(cash, hold + prices[i] - fee); hold = max(hold, cash - prices[i]); } return cash; }