贪心算法也是用来求解最优化问题的,相比较动态规划很多问题使用贪心算法更为简单和高效,但是并不是所有的最优化问题都可以使用贪心算法来解决。
贪心算法就是在每个决策点都做出在当时看来最佳的选择。
贪心算法的设计步骤:
1、将最优化问题转换为:对其做出一次选择之后,只剩下一个问题需要求解的形式(动态规划会留下多个问题需要求解)
2、证明做出贪心选择之后,原问题总是存在最优解,即贪心算法总是安全的
3、证明做出贪心选择后,剩余的子问题满足性质:其最优解与贪心选择组合即可得到原问题的最优解,这样就得到了最优子结构
其中2、3两步主要是为了证明一个问题适不适合使用贪心算法
下面是一个使用贪心算法解决问题的例子:
1、活动选择问题描述
有一个需要使用每个资源的n个活动组成的集合S= {a1,a2,···,an },资源每次只能由一个活动使用。每个活动ai都有一个开始时间si和结束时间fi,且 0≤si<fi<∞ 。一旦被选择后,活动ai就占据半开时间区间[si,fi)。如果[si,fi]和[sj,fj]互不重叠,则称ai和aj两个活动是兼容的。该问题就是要找出一个由互相兼容的活动组成的最大子集。例如下图所示的活动集合S,其中各项活动按照结束时间单调递增排序。
从图中可以看出S中共有11个活动,最大的相互兼容的活动子集为:{a1,a4,a8,a11,}和{a2,a4,a9,a11}。
2、动态规划解决过程
(1)活动选择问题的最优子结构
定义子问题解空间Sij是S的子集,其中的每个获得都是互相兼容的。即每个活动都是在ai结束之后开始,且在aj开始之前结束。假设Aij是Sij的最大的相互兼容的活动子集,再假设ak是Aij中的一个活动,由于最优解包含ak,所以得到了两个子问题寻找Sij中在ak之前的活动中的最优子结构Aik和ak之后的活动中的最优子结构Akj,这样可以得出Aij=Aik∪Akj∪{ak},最优解中活动的个数是|Aij|=|Aik|+|Akj|+1。
下面用剪切-粘贴法证明最优解Aij必然包含其子问题Aik和Akj的最优解。先假设Aij不包含Aik的最优解,那么Aik必然存在一个最优解Aik‘,使得|Aik’|>|Aik|,进而得出|Aik'|+|Akj|+1>|Aik|+|Akj|+1=|Aij|与最初假设的Aij是Sij的最优解冲突,所以最优解Aij必然包含其子问题Aik的最优解。同理证明最优解Aij必然包含其子问题Akj的最优解。
综上最优子结构为:假设Sij的最优解Aij包含活动ak,则对Sik的解Aik和Skj的解Akj必定是最优的。
通过一个活动ak将问题分成两个子问题,下面的公式Aij=Aik∪Akj∪{ak}计算出Sij的解Aij。
(2)一个递归解
设c[i][j]为Sij中最大兼容子集中的活动数目,当Sij为空集时,c[i][j]=0;当Sij非空时,若ak在Sij的最大兼容子集中被使用,则则问题Sik和Skj的最大兼容子集也被使用,故可得到c[i][j] = c[i][k]+c[k][j]+1。
当i≥j时,Sij必定为空集,否则Sij则需要根据上面提供的公式进行计算,如果找到一个ak,则Sij非空(此时满足fi≤sk且fk≤sj),找不到这样的ak,则Sij为空集。
c[i][j]的完整计算公式如下所示:
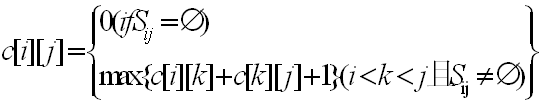
(3)最优解计算过程
根据递归公式,采用自底向下的策略进行计算c[i][j],引入复杂数组ret[n][n]保存中间划分的k值。程序实现如下所示:
1 void dynamic_activity_selector(int *s,int *f,int c[N+1][N+1],int ret[N+1][N+1]) 2 { 3 int i,j,k; 4 int temp; 5 //当i>=j时候,子问题的解为空,即c[i][j]=0 6 for(j=1;j<=N;j++) 7 for(i=j;i<=N;i++) 8 c[i][j] = 0; 9 //当i<j时,需要寻找子问题的最优解,找到一个k使得将问题分成两部分 10 for(j=2;j<=N;j++) 11 for(i=1;i<j;i++) 12 { 13 //寻找k,将问题分成两个子问题c[i][k]、c[k][j] 14 for(k=i+1;k<j;k++) 15 if(s[k] >= f[i] && f[k] <= s[j]) //判断k活动是否满足兼容性 16 { 17 temp = c[i][k]+c[k][j]+1; 18 if(c[i][j] < temp) 19 { 20 c[i][j] =temp; 21 ret[i][j] = k; 22 } 23 } 24 } 25 }
(4)构造一个最优解集合
根据第三保存的ret中的k值,递归调用输出获得集合。采用动态规划方法解决上面的例子,完整程序如下所示:
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 #define N 11 5 6 void dynamic_activity_selector(int *s,int *f,int c[N+1][N+1],int ret[N+1][N+1]); 7 void trace_route(int ret[N+1][N+1],int i,int j); 8 9 int main() 10 { 11 int s[N+1] = {-1,1,3,0,5,3,5,6,8,8,2,12}; 12 int f[N+1] = {-1,4,5,6,7,8,9,10,11,12,13,14}; 13 int c[N+1][N+1]={0}; 14 int ret[N+1][N+1]={0}; 15 int i,j; 16 dynamic_activity_selector(s,f,c,ret); 17 printf("c[i][j]的值如下所示: "); 18 for(i=1;i<=N;i++) 19 { 20 for(j=1;j<=N;j++) 21 printf("%d ",c[i][j]); 22 printf(" "); 23 } 24 //包括第一个和最后一个元素 25 printf("最大子集的个数为: %d ",c[1][N]+2); 26 printf("ret[i][j]的值如下所示: "); 27 for(i=1;i<=N;i++) 28 { 29 for(j=1;j<=N;j++) 30 printf("%d ",ret[i][j]); 31 printf(" "); 32 } 33 printf("最大子集为:{ a1 "); 34 trace_route(ret,1,N); 35 printf("a%d} ",N); 36 system("pause"); 37 return 0; 38 } 39 40 void dynamic_activity_selector(int *s,int *f,int c[N+1][N+1],int ret[N+1][N+1]) 41 { 42 int i,j,k; 43 int temp; 44 //当i>=j时候,子问题的解为空,即c[i][j]=0 45 for(j=1;j<=N;j++) 46 for(i=j;i<=N;i++) 47 c[i][j] = 0; 48 //当i>j时,需要寻找子问题的最优解,找到一个k使得将问题分成两部分 49 for(j=2;j<=N;j++) 50 for(i=1;i<j;i++) 51 { 52 //寻找k,将问题分成两个子问题c[i][k]、c[k][j] 53 for(k=i+1;k<j;k++) 54 if(s[k] >= f[i] && f[k] <= s[j]) //判断k活动是否满足兼容性 55 { 56 temp = c[i][k]+c[k][j]+1; 57 if(c[i][j] < temp) 58 { 59 c[i][j] =temp; 60 ret[i][j] = k; 61 } 62 } 63 } 64 } 65 66 void trace_route(int ret[N+1][N+1],int i,int j) 67 { 68 if(i<j) 69 { 70 trace_route(ret,i,ret[i][j]); 71 if(ret[i][j] != 0 ) 72 printf("a%d ", ret[i][j]); 73 } 74 }
3、贪心算法解决过程
针对活动选择问题,认真分析可以得出以下定理:对于任意非空子问题Sij,设am是Sij中具有最早结束时间的活动,那么:
(1)活动am在Sij中的某最大兼容活动子集中被使用。
(2)子问题Sim为空,所以选择am将使子问题Smj为唯一可能非空的子问题。
有这个定理,就简化了问题,使得最优解中只使用一个子问题,在解决子问题Sij时,在Sij中选择最早结束时间的那个活动。
贪心算法自顶向下地解决每个问题,解决子问题Sij,先找到Sij中最早结束的活动am,然后将am添加到最优解活动集合中,再来解决子问题Smj。
基于这种思想可以采用递归和迭代进行实现。递归实现过程如下所示:
1 void recursive_activity_selector(int *s,int* f,int i,int n,int *ret)
2 {
3 int *ptmp = ret;
4 int m = i+1;
5 //在Sin中寻找第一个结束的活动
6 while(m<=n && s[m] < f[i])
7 m = m+1;
8 if(m<=n)
9 {
10 *ptmp++ = m; //添加到结果中
11 recursive_activity_selector(s,f,m,n,ptmp);
12 }
13 }
迭代实现过程如下:
1 void greedy_activity_selector(int *s,int *f,int *ret)
2 {
3 int i,m;
4 *ret++ = 1;
5 i =1;
6 for(m=2;m<=N;m++)
7 if(s[m] >= f[i])
8 {
9 *ret++ = m;
10 i=m;
11 }
12 }
采用贪心算法实现上面的例子,完整代码如下所示:
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 #define N 11 5 6 void recursive_activity_selector(int *s,int* f,int i,int n,int *ret); 7 8 void greedy_activity_selector(int *s,int *f,int *ret); 9 10 int main() 11 { 12 int s[N+1] = {-1,1,3,0,5,3,5,6,8,8,2,12}; 13 int f[N+1] = {-1,4,5,6,7,8,9,10,11,12,13,14}; 14 int c[N+1][N+1]={0}; 15 int ret[N]={0}; 16 int i,j; 17 //recursive_activity_selector(s,f,0,N,ret); 18 greedy_activity_selector(s,f,ret); 19 printf("最大子集为:{ "); 20 for(i=0;i<N;i++) 21 { 22 if(ret[i] != 0) 23 printf("a%d ",ret[i]); 24 } 25 printf(" } "); 26 system("pause"); 27 return 0; 28 } 29 30 void recursive_activity_selector(int *s,int* f,int i,int n,int *ret) 31 { 32 int *ptmp = ret; 33 int m = i+1; 34 //在i和n中寻找第一个结束的活动 35 while(m<=n && s[m] < f[i]) 36 m = m+1; 37 if(m<=n) 38 { 39 *ptmp++ = m; //添加到结果中 40 recursive_activity_selector(s,f,m,n,ptmp); 41 } 42 } 43 44 void greedy_activity_selector(int *s,int *f,int *ret) 45 { 46 int i,m; 47 *ret++ = 1; 48 i =1; 49 for(m=2;m<=N;m++) 50 if(s[m] >= f[i]) 51 { 52 *ret++ = m; 53 i=m; 54 } 55 }
4、总结
活动选择问题分别采用动态规划和贪心算法进行分析并实现。动态规划的运行时间为O(n^3),贪心算法的运行时间为O(n)。动态规划解决问题时全局最优解中一定包含某个局部最优解,但不一定包含前一个局部最优解,因此需要记录之前的所有最优解。贪心算法的主要思想就是对问题求解时,总是做出在当前看来是最好的选择,产生一个局部最优解。
声明:本文部分内容改自:Anker—学习成长笔记:http://www.cnblogs.com/Anker/archive/2013/03/16/2963625.html
